Você sabe o que está medindo?
Você sabe o que está medindo?
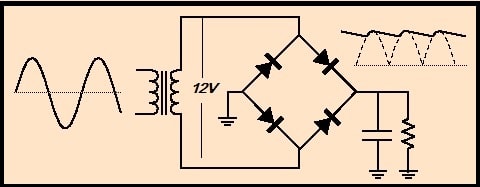
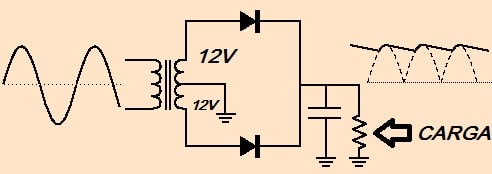
Imagine um circuito bem simples com uma retificação de onda completa que tanto pode ser em ponte (fig.1) ou meia ponte (fig.2), tanto faz, e um capacitor de filtro alimentando uma carga qualquer que será representada aqui por uma resistência.
A “desvantagem”, se assim podemos dizer, da retificação em meia ponte é que obrigatoriamente temos que usar um transformador com derivação central no secundário e por isso, ela nunca é usada em fontes chaveadas, mas afora este detalhe as medidas são basicamente as mesmas.
Suponhamos que você está diante de uma fonte, não tem esquema e muito menos informação sobre a tensão no capacitor de filtro, mas conseguiu medir a tensão nos dois enrolamentos do secundário do transformador ou nas extremidades da ponte (fig.1) e encontrou 12VAC.
Com apenas está informação você saberia dizer qual o valor máximo da tensão DC que deverá aparecer sobre o capacitor de filtro (não confundir com a tensão de isolamento do capacitor)?
Se você respondeu que o valor máximo da tensão DC medida com um voltímetro digital ou analógico deveria ser, tchan, tchan, tchan, 16,92VDC, então meus parabéns. Até aqui você está indo bem.
Voltando à leitura apresentada no voltímetro (16,92V neste exemplo), se você está querendo perguntar “de que cartola saiu este coelho”, eu, embora não seja mágico, respondo que basta multiplicar por 1,41 os 12V AC medidos que vai dar 16,92. Faça a conta e comprove.
Na verdade, na hora de medir você vai achar um pouquinho menos porque tem que descontar cerca de 0,7V da queda de tensão no diodo se o circuito for meia ponte e 1,4V se ponte com quatro diodos.
Se você está querendo saber de onde saiu este 1,41 eu explicarei depois. Por ora vamos ficar com a explicação de que o capacitor de filtro se carrega com o valor de pico da tensão senoidal aplicada ao retificador e manterá este valor em seus terminais, se não houver nenhum consumo de corrente, ou seja, se não estiver alimentando nenhuma carga e para encontrar o valor de pico devemos multiplicar o valor RMS da tensão senoidal por 1,41.
Isto porque os voltímetros “comuns” não indicam o valor de pico da onda senoidal e sim um valor “próximo” ao RMS. Mais adiante falarei do RMS e porque usei a expressão “próximo” quando me referi ao RMS.
Aqui vale uma observação importante. O fator 1,41 só pode ser empregado para determinarmos o valor de pico se a onda for senoidal que é o caso da tensão da rede elétrica mesmo que ela tenha passado por um transformador.
Em outras palavras, se tivéssemos uma onda triangular, por exemplo, que não é o caso, não poderíamos usar 1,41.
Na prática o valor medido será um pouco menor a depender da corrente drenada pela carga que fará com o que capacitor se descarregue um pouquinho entre dois semiciclos daí eu ter dito, lá atrás, que era o “valor máximo”.
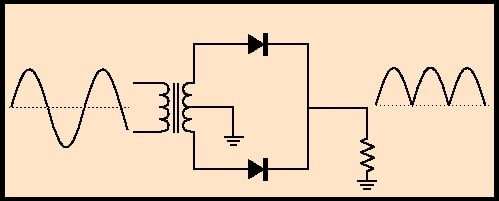
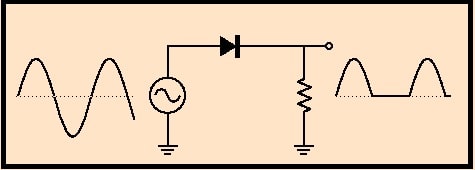
E se o circuito fosse o mostrado na figura 3 onde não temos o capacitor de filtro (suponhamos que ele esteja sem capacitância) qual seria o valor medido na carga ainda usando o voltímetro na escala DC?
Como agora não temos mais o capacitor de filtro para se carregar nós iremos medir o valor médio da tensão pulsante de onda completa que aparece sobre o resistor de carga.
E como calculamos este valor?
Simples, basta multiplicar o valor de pico da senóide por 0,636 e obteremos para o nosso exemplo o valor de 10,76V DC ou cerca de 10V se considerarmos a queda no diodo.
Vale ressaltar que os resultados seriam os mesmos se o circuito retificador fosse em ponte como o da figura 2, salvo o desconto de 1,4V em vez de 0,7V, porque a forma de onda na carga seria mesma nos dois casos.
Neste caso não temos nem uma tensão alternada nem uma tensão contínua e sim uma onda pulsante, mas sempre positiva e se usarmos um voltímetro DC ele medirá a média aritmética de todos os valores da onda que é calculado multiplicando-se o valor de pico por 0,636. Mais adiante vou tentar explicar como se chega a este fator.
Para simplificar nossa sofrida vida de técnico reparador podemos fazer uma conta mais simples, multiplicando o valor RMS da tensão oferecida pelo transformador por 0,9 (que é o resultado aproximado de 1,41 multiplicado por 0,636) e também obteremos o valor médio DC.
Dúvidas prováveis
Se você é um sujeito curioso deve estar querendo saber:
1) O que é valor RMS?
2) De onde surgiu 1,41?
3) De onde surgiu 0,636?
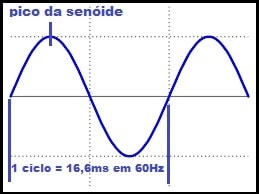
Como você sabe (ou deveria saber) a forma da onda da tensão que é fornecida pelas concessionárias de energia elétrica é sempre senoidal e varia ciclicamente a taxa de 60 vezes por segundo (aqui no Brasil) conforme vemos na figura 4.
Por causa da “velocidade” com que os valores que a tensão assume a cada 16,6 mseg (um ciclo completo) o voltímetro comum não consegue mostrar cada um dos valores assumidos (só o osciloscópio) e por isso, foi necessário “inventar” uma maneira de medir e mostrar a média dos valores a qual recebe o nome de RMS que são as iniciais de Root Mean Square ou Raiz Média Quadrática que também é chamado de valor eficaz e este termo expressa, a meu ver, o significado do valor RMS.
O que se pretende com o valor RMS é encontrar um valor de tensão/corrente alternada que aplicada a uma carga puramente resistiva produza a mesma quantidade de potência que uma tensão ou corrente contínua, portanto constante produziria no mesmo intervalo de tempo, ou seja, com a mesma eficiência ou eficácia que a alternada que é variável e daí surgiu o termo valor eficaz (menos usado) como “sinônimo” para valor RMS.
Eu diria que a expressão valor eficaz expressa a ideia conceitual enquanto o RMS relaciona-se ao processo de cálculo.
O valor RMS é obtido através de uma média dos valores da tensão/corrente alternada, entretanto não podemos fazer uma média aritmética porque o resultado seria nulo uma vez que uma vez que numa senóide cada ciclo é composto de dois semiciclos simétricos.
Por outro lado como o valor eficaz ou RMS de uma senóide é aquele que produzirá a mesma potência que uma tensão/corrente continua e na fórmula do cálculo da potência tanto a tensão ou a corrente aparecem elevadas ao quadrado, daí surge o Valor Médio Quadrático ou Root Mean Square.
Não irei fazer o tratamento matemático aqui por fugir um pouco ao propósito deste artigo, mas apenas informar que é a partir destes cálculos matemáticos que surge o fator 1,41 (que nada mais é que a raiz quadrada do número 2) e por isso que para encontrar o valor de pico da senóide precisamos multiplicar por 1,41 o valor medido pelo voltímetro (digital ou analógico) que é RMS para se chegar ao valor de pico.
Um ponto importante que volto a enfatizar é que este fator 1,41 (que costuma ser chamado de fator de crista) só se aplica a senóide pura.
Vejamos agora o que significa o valor 0,636 que foi citado anteriormente sem entrar na matemática envolvida para se chegar a ele.
Este valor surge da média aritmética “verdadeira” dos valores da forma de onda retificada em onda completa e representa um valor DC, por isso ele aparecerá ao medirmos a tensão sobre a carga no circuito da figura 3 onde não temos o capacitor de filtro.
Os multímetros “comuns” quando na escala de AC utilizam este valor que multiplicado por 1,1 para chegar ao valor “próximo” ao RMS e isto só é verdade se a onda senoidal for pura, ou seja, sem distorções.
Se tivemos cargas reativas, por exemplo, teremos uma “deformação” na senóide e maneira de ter uma medida AC confiável é utilizando um voltímetro TRUE-RMS.
Estes multímetros são muito importantes para eletrotécnicos, mas não chegam a ser indispensáveis no caso da maioria dos reparos de aparelhos eletrônicos a prioridade é a medição de tensões continuas.
Finalmente se em vez de uma onda completa tivéssemos um circuito de meia onda como na figura 5, você seria capaz de dizer por qual fator que deveríamos multiplicar a tensão de pico para se encontrar o valor médio DC da forma de onda sobre o resistor (sem capacitor de filtro)?
É só pensar um pouquinho. Na figura 5 temos a metade da forma de onda afinal é uma retificação de meia onda, logo o fator deverá ser a metade de 0,636 ou 0,318.
Para que você precisa saber estas coisas?
Eu acho que a resposta mais simples é que a partir destes conhecimentos você saberá interpretar os resultados das medidas e concluir o que deve estar errado e porque o circuito não está funcionando corretamente.
Lembre-se de Maxwell: ”Nada mais prático que uma boa teoria”.
Até 2016, ou melhor, até sempre.




8 Comentários