A trigonometria na Eletricidade e na Eletrônica – Parte I
A trigonometria na Eletricidade e na Eletrônica
Um pouco de história (da matemática)
O que para mim é mais fascinante na Matemática é que, quando menos se espera, uma de suas “vertentes” aparece em alguma coisa que estamos estudando e que, nem de longe, poderíamos imaginar que a solução para um problema totalmente novo viesse através de uma “ferramenta” matemática antiga usada para resolver outro tipo de problema.
Não foi a toa que Galileu teria dito que “a matemática é o alfabeto com o qual Deus escreveu o Universo” e concordo plenamente que a matemática está sempre presente na Natureza, seja lá “quem” a usou-o para “escrever” o Universo.
Se você é um estudante de Eletricidade ou Eletrônica certamente já ouviu falar em seno e cosseno que são assuntos que fazem parte do ramo da matemática chamado trigonometria.
Pois a trigonometria é mais um destes casos de alguém que atirou no que viu e acertou no que não viu. Ela não nasceu pronta e acabada e não teve um único “inventor”, mas atribui-se a um sujeito chamado Hiparco lá pelo século II aC a “paternidade” da trigonometria ao ter construído uma tabela que relacionava o comprimento de uma corda de circunferência com ângulo subentendido por esta corda.
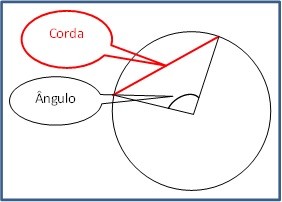
Talvez valha a pena lembrar que a corda da qual estou falando aqui não pretende enforcar ninguém e sim, refere-se ao segmento de reta que une dois pontos quaisquer de uma circunferência como aparece na figura.
Por este feito, Hiparco é considerado o “pai” Trigonometria (ela, a trigonometria, não teve mãe!).
É bem provável que você talvez nunca tenha visto uma abordagem da trigonometria sobre este “ângulo” (sem trocadilho) que eu vou apresentar aqui. Devem ter lhe dito (se disseram) lá no ensino médio que “tri-gono-metria” quer dizer “medida dos três lados” e estamos conversados.
Ora se tem três lados então deve ser um triângulo, e o que a “corda” de uma circunferência tem a ver com um triângulo e para que Hiparco queria uma tabela que relacionasse a corda de uma circunferência com o ângulo dentro desta circunferência ?
A tabela de Hiparco ajudava-o a resolver os “seus” problemas de astronomia como a distância da Terra a Lua ou ao Sol e outros similares.
E o que isso tudo tem a ver com a Eletricidade e a Eletrônica que nem sonhavam existir no século II aC?
É, parece que Galileu tinha mesmo razão e é por isso que sou fã dele. Coisas aparentemente distintas no Universo acabam tendo soluções através de um mesmo conceito matemático. A trigonometria é só um exemplo.
Quer outro? Os logaritmos. Já ouviu falar deles?
Os logaritmos aparecem na Eletrônica numa unidade chamada decibel da qual certamente você já ouviu falar. Mas isto é assunto para outro artigo, por ora vamos nos concentrar na trigonometria.
Entretanto, a trigonometria como a estudamos hoje sofreu algumas “mutações” na ideia primitiva de Hiparco que foram introduzidas pelos hindus no final do século IV num texto chamado Sidhanta que quer dizer Sistema de Astronomia (não confundir com Astrologia, por favor).
Até então a obra máxima da astronomia era o Almajesto, do grego Ptolomeu, que significa Coleção Maior ou O Grande Tratado.
Só no século VIII, já da era cristã, a trigonometria dos hindus começou a ser percebida pelos “cientistas” da época que descobriram que os hindus em vez de trabalhar com a corda de Hiparco preferiram trabalhar com metade da corda. Uma grande sacada que consolidou a trigonometria como a estudamos atualmente.
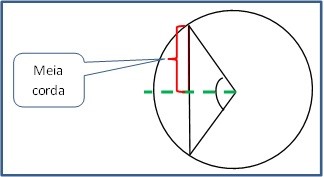
Acompanhe na figura 2.
Observe que ao dividir a corda ao meio passamos a ter dois triângulos com uma caraterística muito especial: são triângulos retângulos.
Mais tarde, por volta do ano 850, o matemático árabe al-Batani introduziu uma nova ideia ao “método hindu” e além de utilizar a meia corda passou a trabalhar com o raio da circunferência sempre igual a um.
A origem da palavra seno
O Siddantha dos hindus era escrito em sânscrito e nele a meia corda era denominada jiva que foi traduzida para o árabe como jiba, foi abreviada por jb e terminou sendo interpretada como jaib que significa “peito”. No século XII o texto foi traduzido para o latim por Gerard Cremona que utilizou a palavra sinus como equivalente de “peito”. Em 1590 o matemático inglês Robert de Chester (que não é aquele que se come no Natal) introduziu o termo sine que é usado até hoje em muitos livros. Daí para chegar a seno em português foi só um pulo.
Não é a toa que existe um trocadilho italiano que diz:Traduttore, Traditore , traduzindo (ou traindo!) para o português: Tradutor, Traidor!
A definição “moderna” para seno de um ângulo
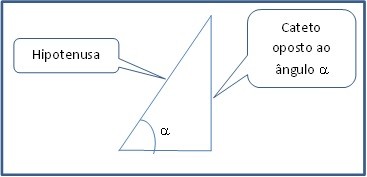
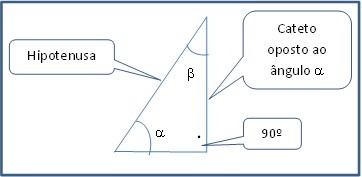
No ensino médio estuda-se que o seno de um ângulo é o resultado da divisão do cateto oposto a este ângulo pela hipotenusa do triângulo retângulo.
Repare que o cateto oposto ao ângulo a corresponde a “meia corda” que os hindus chamavam de jiva e depois de sucessivas traduções (ou traições) acabou virando seno.
Observe ainda que o que chamamos de hipotenusa do triângulo é o raio da circunferência usada para obter-se a corda ou meia corda que al-Batani considerava como unitário.
A grande sacada dos hindus ao usar a meia-corda eles foi obtiver um triângulo retângulo e aí poder associar o famoso Teorema de Pitágoras à trigonometria. Viu como uma coisa leva a outra. Viva Galileu!
E para que serve tudo isto?
Você pode achar que não, mas já vou lhe mostrar como esta “invenção” que começou com Hiparco irá simplificar muito os cálculos de muita coisa que envolva ângulos e mais adiante mostrarei também como isto irá cair na Eletricidade.
Medir ângulos não é uma tarefa tão simples como medir segmentos de reta, assim se tivermos uma tabela que relacione cada ângulo com seu seno tudo ficará mais fácil.
O trabalho “pesado” será feito só uma vez para construir a tabela e depois basta usá-la para encontrar o valor de qualquer ângulo uma vez que conheçamos o valor do seno deste ângulo que pode ser calculado dividindo-se o cateto pela hipotenusa de um triangulo retângulo que contenha o ângulo procurado.
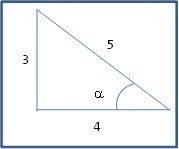
Vamos a um exemplo. Imagine um triângulo retângulo como o mostrado na figura 4.
Não sabemos o valor do ângulo a , mas podemos calcular o seu seno dividindo o cateto oposto a ele que neste caso vale 3 pela hipotenusa que vale 5. Logo sen a = 3 / 5 = 0,6.
Agora poderemos recorrer a uma tabela trigonométrica e descobriremos que o ângulo a vale aproximadamente 37º.
Na verdade, o hoje em dia não precisamos mais recorrer às tabelas porque as calculadoras já nos dão estes valores, mas não tratarei disto aqui.
Vamos aproveitar que já estamos com a mão na massa e tratar logo de uma “entidade” da trigonometria da qual você já deve ter ouvido falar também: o cosseno de um ângulo que costuma ser abreviado por “cos”.
Relembrando conceitos de geometria
Antes de tratar do cosseno talvez valha a pena relembrar algumas coisinhas de geometria nos triângulos.
A primeira delas é que a soma dos três ângulos internos de qualquer triângulo é sempre igual a 180º.
No momento estamos interessados no triângulo retângulo que por construção têm um ângulo reto que, portanto vale 90º.
Logo, a soma dos outros dois ângulos do triângulo retângulo dará sempre 90º.
Outra coisa que precisamos saber é que quando a soma de dois ângulos dá 90º eles são chamados ângulos complementares.
Bingo! Então aquele “co” no termo cosseno quer dizer “complementar”?
Muito bem, eu sabia que você iria perceber isso.
As definições de seno e cosseno para uso prático
Até aqui eu fiz toda uma caminhada histórica para chegar a estas conclusões porque acho bastante interessantes saberemos que as coisas não caem do céu prontas e acabadas (só a chuva).
Para efeitos práticos você pode até “esquecer” tudo que dito até aqui, mas precisa memorizar para o resto da sua vida as duas informações que virão a seguir.
Além disso, olhando a figura 5, é fácil perceber que num triângulo retângulo
 uma vez que a soma dos dois sempre dá 90º.
uma vez que a soma dos dois sempre dá 90º.
Para finalizar esta primeira parte é importante deixar umas das relações mais importantes da trigonometria que nos dá:
Mas de cartola saiu este coelho, você deve estar querendo perguntar?
Ora, das cartolas do árabe al-Batani que “decretou” que o raio da circunferência seria unitário e do grego Pitágoras com seu famosíssimo teorema que diz de forma resumida na versão popular que a “soma dos quadrados dos catetos é igual ao quadrado da hipotenusa”.
Nas expressões para seno e cosseno através das relações entre os lados de um triângulo retângulo que foram mostradas acima (amarelo e verde) se fizermos a hipotenusa igual a 1 passamos a ter sen α = cateto oposto e cos α = cateto adjacente.
Acompanhe na figura abaixo
Aplicando o Teorema de Pitágoras ao triângulo acima obteremos uma das relações mais utilizadas em todos os problemas que envolvam este conceitos básicos da trigonometria que começaram a ser pensados pelo homem lá no século II ac (ou antes) e chagaram até o século XXI para , entre outras coisas, ajudar a mandar o homem à Marte (a Lua ele já foi)!
No próximo artigo ainda ficaremos aqui pela Terra mesmo e veremos com a trigonometria foi parar na Eletricidade.
Aguardem, vai ser emocionante.







8 Comentários