Operador J, você sabe o que é isso?
Há algum tempo um aluno do Clube Aprenda Eletrônica com Paulo Brites pediu-me que eu escrevesse alguma coisa sobre “operador j”, pois ele não entendia bem o que era e para que servia.
Resolvi então, que talvez valesse a pena dividir esta explicação com os leitores do blog. Mãos à obra!
Pretendo tratar deste assunto com mais profundidade em um livro que estou preparando sobre matemática para Eletricistas e Técnicos em Eletrônica, mas por enquanto vou dar apenas um spoiler que servirá como uma introdução ao tema.
De maneira bem suscinta, pode-se começar por dizer que o operador j é um método para simplificar os cálculos em circuitos de corrente alternada e foi proposto pelo matemático e engenheiro eletricista alemão Charles Proteus Steinmetz (1865-1923).
Os cálculos de circuitos em corrente alternada podem se tornar bastante trabalhosos se utilizarmos apenas geometria e trigonometria e, para simplificá-los, Steinmetz teve a brilhante ideia de utilizar a notação de “números” complexos.
Reparou que coloquei a palavra números entre aspas?
Este assunto faz parte do currículo de matemática do Ensino Médio e provavelmente, ao se deparar com o termo pela primeira, o estudante poderá sofrer por antecipação (e até ficar com complexo de inferioridade, no sentido psicológico!), pensando que, por ser “complexo”, deverá ser de difícil compreensão e terá dificuldade para aprender.
Todavia a palavra “complexo”, neste caso, não é um adjetivo e sim, um substantivo.
Estou sempre batendo nesta tecla de que ao estudar qualquer coisa nova deve-se começar pela etimologia da palavra “estranha” que apareceu a nossa frente.
Você foi ao médico e ele lhe receitou um “um complexo de vitaminas” que, neste caso, significa um “combinado” de vitaminas.
E é assim que devemos entender os “números” complexos, um “combinado de números”. Simples assim! Já pode cancelar a consulta com o psicólogo!
Alguns livros de matemática também o chamam de “números imaginários” para distingui-los dos “outros”: – os chamados números reais que, provavelmente você também não saiba muito bem o que é, mas já se acostumou com o termo.
Complexos e imaginários: – como tudo começou
Quando começamos a estudar a resolução das equações do segundo grau, pelo método decoreba da tal da “fórmula de Baskara”, em um determinado momento, nos deparamos com uma situação “complexa”, neste caso “adjetivisticamente falando”, no sentido de difícil solução.
Isto acontece quando aparece um “número real negativo” cuja raiz quadrada precisamos “extrair”.
Provavelmente, os seus professores lhe disseram algo como “não há solução no campo dos números reais” e que, “mais tarde”, você iria ter “contatos imediatos” com os números complexos ou imaginários.
Alguns professores mais dedicados e a depender do nível de interesse dos alunos, costumavam preparar o “terreno” dando um spoiler sobre o “futuro”.
Se aparecesse a raiz quadrada de -4, por exemplo, eles reescreviam como (4).(-1) e aí extraia-se a raiz do 4 (positivo) nos dando (+/- 2), enquanto o (-1) ficava “intocável” debaixo do símbolo de radiciação ![]()
Uma maneira, sutil, como eu disse, de prepará-lo para o contato com os “números complexos ou imaginários”, quando você estiver “grandinho(a)” suficiente para entender estas “coisas” lá no Ensino Médio.
Ao chegar no Ensino Médio dizem para você que, por uma questão de simplificação, em vez de escrever “raiz quadrada de -1“, vamos utilizar a letra i minúscula em seu lugar. Você já concluiu, com a genialidade peculiar aos meus leitores, que a letra i, neste caso, neste caso, vem de imaginário.
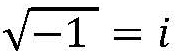
Vamos a um exemplo.
Suponhamos que ao tentar encontrar as raízes de uma determinada equação do segundo grau você chegou a: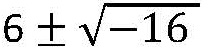
Usando a “técnica” explicada anteriormente, escreveu![]()
Começou a perceber por que o tal “número complexo” se comporta como um “combinado” de dois números?
Do lado esquerdo temos a “parte real” e do lado direito, o tal do número imaginário. Os dois “vivem juntos”, mas separados e como água e óleo, não se “misturam”.
E agora vou lhe contar um segredinho.
Se estivermos trabalhando com circuitos elétricos e algo deste tipo acontecer, em vez de usar a letra i, passamos a usar a letra j (minúscula).
Em eletricidade a letra i é usada, universalmente, para representar a intensidade da corrente elétrica, seja AC ou DC.
Assim, para evitar confusões entre “corrente” e “imaginário” fica combinado que os matemáticos utilizarão a letra i, enquanto os eletricistas darão preferência pelo j.
Em outras palavras, os matemáticos escrevem 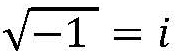
e na engenharia elétrica se escreve
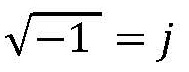
Ah! Então, é isso que é o operador j?
Não exatamente. Só mais um pouquinho de suspense e o mistério será revelado.
Uma rápida abordagem sobre o Diagrama de Argand
Antes de chegarmos ao operador j, precisamos estudar mais umas coisinhas. Comecemos com o Diagrama de Argand.
Este diagrama, nada mais é uma adaptação das coordenadas cartesianas ou coordenadas retangulares e que irá permitir que façamos uma interpretação geométrica do significado de um número complexo.
Essa é a beleza da matemática, fazer com que coisas, aparentemente dispares, se conectem. Pense nisso!
O, bem conhecido, sistema de coordenadas cartesianas ou retangulares é composto, como se sabe, por duas linhas perpendiculares que se cruzam e são denominadas Eixo Horizontal e Eixo Vertical.
Na matemática formal os Eixos Horizontal e Vertical são designados, respectivamente, pelas x e y.
A grande sacada do Argand foi renomear estes eixos da seguinte maneira: – o eixo horizontal passa a ser utilizado para representar a “parte real” do número complexo, enquanto o eixo vertical será denominado de eixo j (ou i) e nele representaremos a “parte imaginária” do número complexo.
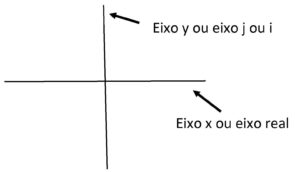
Fig. 1 – Diagrama de Argand
Acompanhe na fig.2 a representação de alguns números complexos no Diagrama de Argand.
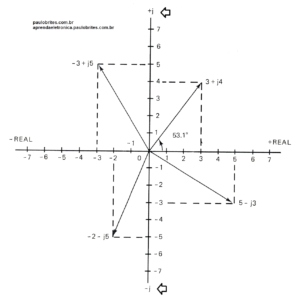
Fig.2 Alguns números complexos no Diagrama de Argand
O operador j
Vamos dar uma interpretação geométrica para a representação de um número complexo no diagrama de Argand.
“Multiplicar” um número real por j, fará ele girar 90° no sentido contrário aos ponteiros do relógio.
A palavrar “multiplicar” não se adapta bem aqui e por isso, coloquei entre aspas.
Melhor seria dizer: – aplicar o operador j a um número real fará ele girar 90° no sentido contrário aos ponteiros do relógio (quando eles eram analógicos!).
Em outras palavras, j = faz uma operação de rotacionar 90° num valor que “real” levando-o para o eixo “imaginário”.
E se aplicarmos o j novamente o que acontecerá?
Considerando j como um operador que rotaciona 90° teremos j x j = j2 = – 1 e portanto, irá cair no lado negativo do eixo real.
Mais uma aplicação do operador j e teremos j3 = j2 x j = – j levando para parte negativo do eixo imaginário.
E finalmente j4 = j2 x j2 = 1, retornamos à parte positiva do eixo real.
Acompanhe na Fig.3
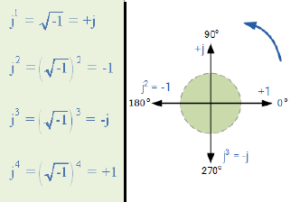
Fig. 3 – Operador J
O que o operador j tem a ver com circuitos de corrente alternada?
Lembre-se que quando uma tensão alternada senoidal é aplicada a um indutor ou a um capacitor a corrente e a tensão não estarão em fase como ocorre num elemento puramente resistivo.
No caso da indutância a corrente ficará 90° atrasada da tensão como vemos na fig.4.
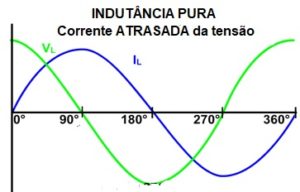
Fig. 4 – Defasagem ni Indutor
Quanto ao capacitor teremos a tensão atrasada da corrente ou também podemos dizer que a corrente está adiantada da tensão a depender da grandeza elétrica que usarmos como referência.
Acompanhe na Fig.5.
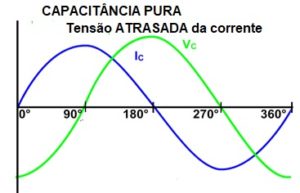
Fig. 5 – Dafasagem no capacitor
Considerado que o operador j funciona como uma “entidade” matemática que produz rotações de 90° parece-nos que ele seria um bom candidato a resolver e simplificar a resolução de problemas em circuitos de corrente alternada.
Resta agora usar a imaginação e ver como podemos juntar os números complexos que surgiram para resolver algumas equações do 2º segundo com algo aparentemente desconectado que são os circuitos elétricos.
Como disse Steve Jobs, está aí no mundo a nossa disposição, basta sabermos ligar os pontos e criar coisas novas.
Quando eu comecei esta explanação, mencionei que “os cálculos de circuitos em corrente alternada podem se tornar bastante trabalhosos se utilizarmos apenas geometria e trigonometria” e que Steimetrz desenvolveu um método para simplificar estes cálculos utilizando a notação dos números complexos.
O operador j foi um passo importante, mas precisamos introduzir mais um conceito para conseguirmos simplificar as contas.
O conceito de fasor
Você, provavelmente, já ouviu falar em vetores e se não ouviu CLIQUE AQUI, para ver uma aulinha sobre assunto.
Olhando o diagrama da fig.2 as setas que representam cada um dos números complexos lembram vetores que podem ser expressos analiticamente de duas maneiras.
Uma delas é a magnitude da grandeza física e a direção que ela assume (ângulo em relação ao eixo horizontal).
Pode-se também usar as projeções do vetor nos eixos x e y.
Na verdade, um fasor é quase a mesma coisa que um vetor.
O fasor será expresso na forma retangular usando o operador j.
Vou tentar explicar isso de uma forma melhor.
Imagine que queremos representar a impedância de um circuito RC ou RL usando o Diagrama de Argand.
O eixo horizontal será usado para representar a parte resistiva do circuito (real do número complexo).
A parte reativa (capacitiva ou indutiva) será representada no eixo vertical, agora chamado eixo j (imaginária do número complexo).
Veja a fig. 6.
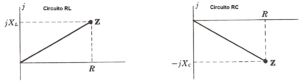
Fig. 6 – Diagrama fasorial de circuito RL e RC
Com este “artifício” podemos escrever as impedâncias como
Z = R + j XL e Z = R – j XC
Estas maneiras de escrever são chamadas de forma retangular e ajudam muito a resolver os circuitos porque somar e subtrair números complexos é uma atividade bem simples.
Entretanto, elas não se tornam muito amigáveis quando precisamos, multiplicar e dividir, por exemplo.
Para sanar o problema lançamos mão de um outro modelo chamado forma polar.
Na forma polar utilizamos a magnitude de Z, obtida com o Teorema de Pitágoras e o ângulo de defasagem.
Não irei tratar aqui da parte de cálculos que ficará para o livro.
O objetivo deste post foi apresentar e desmistificar o conceito de operador j.
Espero ter conseguido.
Com a palavra os leitores nos comentários, sempre bem vindos.
Seja um PATROCINADOR do site para ajudar a mantê-lo no ar.





2 Comentários