Considerações práticas sobre Correção do Fator de Potência
Considerações práticas sobre Correção do Fator de Potência
De uns tempos para cá a correção do fator de potência ficou em evidência e virou a “fórmula mágica” para diminuir o valor da “conta de luz” que passou a tirar o sono das pessoas por causa do tarifaço pós-reeleição.
Em diversos posts anteriores já escrevi sobre correção do fator de potência, mas mesmo assim a coisa ficou mais no campo da teoria, pensei então que seria hora então de juntarmos a teoria com a prática e mostrar que os “amuletos” vendidos pela Internet para uso doméstico a fim de efetuar a correção do fator de potência e, como consequência, baixar a conta não passam de uma fraude.
A proposta deste artigo é meramente didática e pretende demonstrar como podemos determinar o fator de potência e a consequente correção dele utilizando apenas um voltímetro digital que, no meu caso, será o Fluke 107.
A partir daí você irá concluir que não existe um aparelhinho mágico que resolve todos os problemas, porque cada caso é um caso.
Por outro lado o consumo “extra” ocasionado por um fator de potência baixo (na prática menor que 0,92) não é levado em consideração nas contas de energia elétricas domésticas, logo usar o aparelhinho ou colocar um galho de arruda junto da tomada terá o mesmo efeito!
Encontrando o fator de potência
O ideal seria utilizarmos um analisador de qualidade de energia como o Fluke 435, por exemplo, que já nos dá todas as informações na tela, mas ele está fora do alcance (e do bolso) da maioria dos mortais aqui no Brasil, inclusive do meu. Por outro lado, sob o ponto de vista de entender profundamente conceitos, um trabalho como este, certamente, ajudará bastante.
O processo exigirá a realização de três medições (por isso, conhecido como método dos três multímetros) e alguns cálculos o que dará ao leitor uma boa oportunidade de, volto a repetir, entender claramente o conceito de potência em corrente alternada.
Melhor seria utilizar três instrumentos, de preferência iguais e TRUE RMS, mas como diz o ditado – quem não tem cão caça como gato – eu utilizei apenas um, o Fluke 107, para fazer uma medida de cada vez.
Quando comecei a escrever este artigo iniciei uma busca na Internet para ver se já havia algum trabalho (em português) que fosse realmente esclarecedor, pois se já existisse não valeria a pena o meu esforço. Seria, como diz o dito popular, “chover no molhado”.
Encontrei vários artigos, mas sem muito aprofundamento e até coisas com procedimentos que não levam a resultados corretos, por isso resolvi “pegar o touro pelos chifres” o que me levou ao post que ora apresento.
Nada mais prático que uma boa teoria, já dizia Maxwell.
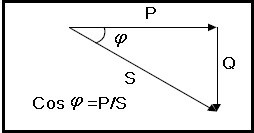
Sendo assim, não custa relembrar que num circuito AC com cargas reativas (indutores e/ou capacitores) temos três “tipos” de potências envolvidas: real ou ativa (medida em W), reativa (medida em VAr) e aparente (medida em VA).
Tabela de potências em CA
É usual representar-se cada uma destas potências por uma letra para facilitar a construção de um triângulo equilátero chamado de “triângulo das potências” que será utilizada para os nossos cálculos e conclusões.
A potência real ou ativa representada por P e medida em watts está em fase com a corrente no circuito, por isso a colocamos na horizontal e a potência reativa (Q) medida em volt-amperes reativos estará defasada 90º de P ficará na vertical. Finalmente a potência aparente (S) medida em volt-amperes é a soma vetorial de P e Q será a hipotenusa do triângulo retângulo aqui denominado triângulo das potências.
Triângulo das potências
Aplicando o Teorema de Pitágoras ao triângulo das potências temos
Fórmula para cálculo da potência reativa
Guarde esta expressão, pois iremos utilizá-la mais adiante para encontrarmos a potência reativa (Q).
Precisaremos também do conceito de cosseno de um ângulo a partir de um triângulo retângulo como o nosso triângulo das potências.
Cos fi
O cosseno do ângulo entre a potência real (P) é a potência aparente (S), geralmente designado pela letra grega “fi” (Φ) é o chamado Fator de Potência e pode ser calculado dividindo-se o valor de P por S.
Feita esta mini revisão de conceitos matemáticos vamos à prática.
O que sabemos do nosso equipamento?
O fabricante dos equipamentos, geralmente, nos informa apenas o valor de P em watts. Pode ser que, às vezes, o valor de S em VA também seja indicado bem como o fator de potência, entretanto para fazer a correção do fator de potência precisamos saber o valor de Q, pois a partir dele saberemos o quanto de reatância o circuito está oferecendo já que é ela que está diretamente relacionada à potência reativa Q expressa em VArs é que é a “vilã” da história.
No caso de um motor temos reatância indutiva (XL) e para “neutralizar” seu efeito no circuito coloca-se um capacitor em paralelo que ofereça uma reatância capacitiva (XC) de mesmo valor que a indutiva (XL).
Vamos nos prender ao caso mais comum: só sabemos o valor da potência ativa em watts e mais nada.
Descobrindo o valor de Q
E aqui precisamos tomar cuidado, aliás, este foi um dos erros encontrado num trabalho apresentado na Internet.
Não podemos considerar o valor de potência real (P) informado pelo fabricante como referência para os nossos cálculos, porque ele é um valor aproximado.
Por exemplo, se estivermos falando de um motor, a potência irá variar se o motor está com ou sem carga, então precisaremos medir a potência da nossa cobaia para uma determinada condição.Vejamos isto na prática tomando como exemplo um ventilador, que é uma carga indutiva e, portanto reativa. O fabricante da nossa “cobaia” só informou na sua etiqueta o seguinte: 127V – 30W.
A primeira coisa que vamos fazer é descobrir a corrente que o motor está “puxando” da rede. Parece fácil, não é? Basta colocar um amperímetro em série com o ventilador e medimos a corrente, certo?
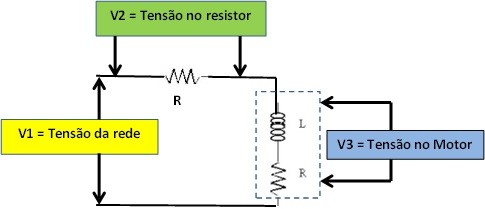
Podemos também montar o circuito abaixo que consiste em colocar um resistor de valor conhecido em série com o motor (no caso o ventilador) e efetuar três medidas: V1, V2 e V3.
Como o circuito é série a corrente no resistor é a mesma no motor e pode ser encontrada com o auxílio da boa e velha Lei de Ohm dividindo V2 por R.
Circuito para medir corrente e tensão
Até aqui tudo bem. Se multiplicarmos a corrente no circuito pela tensão aplicada (V1) obteremos o valor da potência, mas qual delas: P, S ou Q?
Em um circuito de corrente alternada, sempre que multiplicamos a tensão aplicada pela corrente no circuito obtém-se a potência aparente (S).
Se o circuito fosse puramente resistivo (um chuveiro elétrico, por exemplo) a potência aparente (S) coincidiria com a potência real (P), já que não haveria potência reativa, mas não é este o nosso caso.
Fazendo as medições
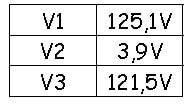
Utilizei um resistor de 10 ohms em série, para facilitar as contas, e obtive o seguinte resultado no Fluke 107:
Medidas de tensão
A partir daí conclui-se facilmente que I = V2/R = 3,9V/ 10Ω = 0,39A.
Agora que sabemos o valor de I podemos encontrar S multiplicando V1 por I e obteremos S = 125,1V x 0,39A = 48,8 VA.
Para determinar o valor de Q utilizaremos
Fórmula para cálculo da potencia reativa
(eu disse que iríamos utilizá-la).
Mas, pera aí, falta determinar o valor de P e para isto poderíamos pensar em multiplicar V2 por I, por exemplo, entretanto aqui há um pequeno problema, estaríamos desprezando a resistência interna do motor.
Lembre-se que a soma de V2 com V3 corresponde a V1, mas que esta soma não é aritmética e sim vetorial como vemos na figura abaixo.
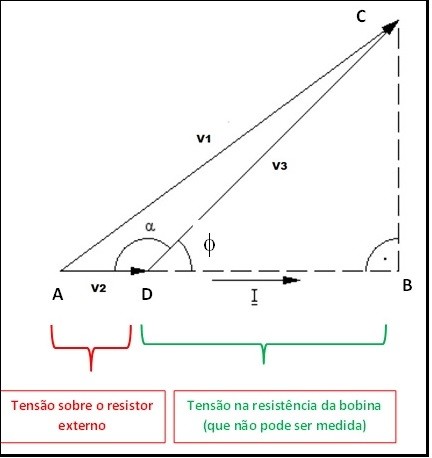Além disso, repare que o triângulo obtido com as tensões V1, V2 e V3 não é um triângulo retângulo o qual precisamos para encontrar o ângulo Φ que dá a defasagem entre potência real e a potência aparente e cujo cosseno é o procurado fator de potência.
Para resolver este impasse vamos “esticar” o lado do triângulo onde está V2 (segmento de reta AD) e baixar uma perpendicular a partir do vértice C que irá produzir o ponto B.
Pronto, agora temos um triângulo retângulo (DCB) e o ângulo Φ que estávamos querendo.
Devemos admitir que dizer que o cosseno “deste” Φ é o fator de potência é “forçar um pouco a barra”.
Alguém consegue perceber por quê?
O “gato escondido” foi o resistor externo acrescentado ao circuito, por isso quanto menor o seu valor em relação à resistência da bobina melhor.
Repare que se o resistor externo fosse igual a zero, V2 também ficaria valendo zero fazendo V1 ficar igual a V3, mas aí caímos numa cilada pois não temos como medir a tensão na resistência da bobina (segmento DB do nosso triângulo retângulo).
O jeito foi aplicar este artifício que embora vá nos fornecer um valor do fator de potência um pouquinho errado é uma alternativa para quem não tem dinheiro para comprar o Fluke 435, além de ser um ótimo exercício para entender conceitos.
Descobrindo o valor do cos Φ
Olhando o nosso triângulo e aplicando a trigonometria temos cos Φ = DB /V3.
Aqui vou abrir um parêntese para uma perguntinha. Qual o significado “elétrico” do lado DB do nosso triângulo?
Voltando a Terra! Até aqui está tudo muito bem (assim espero), mas temos um novo problema. Não sabemos o valor de DB que é a tensão na resistência da bobina. Chi! Acabei de responder a pergunta acima.
Não criemos pânico, novamente aplicando a Lei dos Cossenos da boa e velha “trigonô” ao triângulo não retângulo ADC teremos
(V1)2 = (V2)2 + (V3)2 – 2 V2 x V3 cos α
Ops! Esta relação está nos dando cos α e nós queremos cos Φ.
Isso é mole de resolver.
Repare que α = 180 – Φ, portanto: cos 180 – Φ = – cos Φ.
Nossa expressão poderá ser reescrita como
(V1)2 = (V2)2 + (V3)2 – 2 V2 x V3 (- cos Φ)
e finalmente dando algumas cambalhotas algébricas … tchan, tchan, tcan eis o nosso “procurado” fator de potência, vulgo cos Φ.
Resumindo o que você vai precisar mesmo é da expressão abaixo.
Fórmula para cálculo do cos fi
Fazendo as contas
Agora bastará substituir os valores medidos e encontraremos
cos Φ = (125,12 – 3,92 – 121,52) / 2 x 3,9 x 125,1 = 0,894
Descoberto que o fator de potência é 0,894 podemos encontrar a potência real “verdadeira”.
Basta lembrar que cos Φ = P/S e o valor de S foi o primeiro item que calculamos como igual a 48,8VA teremos, P = S cos Φ = 48,8 x 0.89 = 43,6W, ou seja, cerca de 45% maior que o informado pelo fabricante!
O próximo passo do cálculo será encontrar o valor de Q (potência reativa) que pode ser conseguida aplicando a fórmula que eu disse que seria utilizada
Fórmula para cálculo da potencia reativa
e obteremos Q = 21,92VAr
Vamos tentar corrigir o fator de potência?
Segundo a NBR5410 o fator de potência deve ser no mínimo, 0,92. O valor do fator de potência do nosso ventilador cobaia calculado como 0,894 já esteja muito próximo deste número, apenas como um exercício didático vamos tentar chegar ao valor recomendado.
Relembrando que o objetivo de corrigir o fator de potência é eliminar ou diminuir a potência reativa e neste caso consistirá em colocar em paralelo com a bobina do ventilador um capacitor que ofereça uma reatância capacitiva (XC) de mesmo valor que a reatância indutiva (XL) do motor do ventilador, logo o primeiro passo é descobrir o valor da reatância indutiva.
Como já sabemos o valor da potência reativa (Q) a partir da expressão básica para o cálculo de potência, neste caso reativa, temos
Calculo de Q
da qual tiramos que
Fazendo as contas obteremos XL= 121,52/21.92 = 673,46 ohms.
O cálculo da reatância capacitiva (XC) é feito pela relação Xc= 1/2πfC .
Fazendo algumas manipulações algébricas e substituindo f por 60Hz e 2π por 6,28 chegamos a uma maneira rápida de encontrar C em microfarads pela fórmula: C = 2654/XC.
Como o valor de XC adotado para encontrar C deverá ser igual ao valor de XL que calculamos anteriormente teremos C = 2654/673,46 =4µF (aproximadamente).
Da teoria para a prática (até que em fim)
O próximo passo será colocar um capacitor do valor calculado acima (ou próximo) em paralelo com o nosso ventilador e voltar a fazer a medida da corrente no circuito.
Se tudo estiver certo esta corrente deverá cair indicando que a potência reativa diminuiu (o ideal seria chegar à zero).
Como o nosso fator de potência já estava muito próximo de 1 não obteremos uma redução significativa da corrente, mas de qualquer forma o novo valor de tensão que eu medi sobre o resistor de 10 ohms passou para 3,5V indicando que a corrente caiu de 0,39A para 0,35A.
Resumo da ópera
Para quem tiver interesse em verificar estes resultados fazendo experiências dou a seguir uma “receita de bolo” para que você não precise seguir todos os passos do artigo.
Montado o circuito faça uma tabela com as medidas de tensão conforme sugerida a seguir.
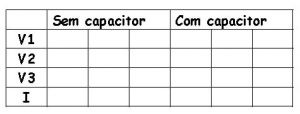
1) Calcule a corrente I = V2/R
2) Calcule a potência aparente S = V1 x I
3) Calcule o cos Φ (fator de potência) usando a fórmula
Fórmula para cálculo do cos fi
4) Calcule P = S cos Φ
5) Calcule Q
Fórmula para cálculo da potencia reativa
6) Calcule XL
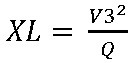
7) Calcule C = 2654/XL (o valor já estará em microfarads).
8) Coloque um capacitor de valor aproximado ao calculado em paralelo com o motor e refaça as medidas completando a tabela.
Obs. O capacitor não pode ser eletrolítico.
Considerações Finais
Dois foram os meus objetivos principais com este artigo. O primeiro deles foi provar que os “amuletos” vendidos por aí são uma fraude, já que cada caso é um caso, portanto não existe o aparelhinho que resolve tudo.
O segundo foi apresentar uma revisão de conceitos sobre potências em AC que pode ser útil para estudantes de eletricidade e para quem está se preparando para concursos nesta área.
A implantação de capacitores para correção de fator de potência é importante para grandes consumidores e precisa ser feita por um profissional qualificado o que não é o objetivo deste artigo.
O artigo em pauta dá apenas noções preliminares sobre o tema, embora tecnicamente corretas.
Finalmente, gostaria de enfatizar que este foi um dos artigos mais trabalhosos que escrevi e estou, há alguns meses, trabalhando nele, pois tive a preocupação de ser o mais didático possível, ou como me disse uma vez meu inesquecível professor PBO : “informar sem mutilar”.
Não sou engenheiro eletricista, mas espero não ter cometido nenhum erro conceitual. Se, por ventura, o fiz aceito as críticas e este espaço está aberto para comentários elucidativos sobre o tema.
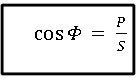
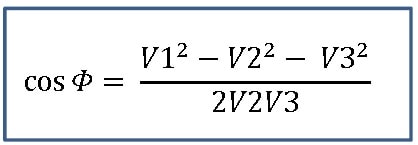
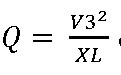
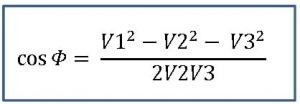
6 Comentários