E Deus disse “façam-se os bits” e assim surgiu a Eletrônica Digital! – Parte I
Resolvi escrever uma série de posts sobre introdução a Eletrônica Digital, principalmente, por causa de um comentário de um leitor em “Amplificadores digitais, ouvidos analógicos”.
Vamos ao comentário do leitor Carlos: “Muito bom este artigo. Só uma dúvida, como é feita a modulação de analógico para digital, se analógico é senoidal e o digital, no caso, os pulsos são largos e estreitos? É isso? Só não sei como o circuito faz isso.”.
A dúvida do Carlos é bastante pertinente (ele usou o termo modulação indevidamente, depois veremos isto) e creio que pode ser a de muita gente, que ficou com vergonha de pagar mico e levantar o dedinho pra dizer “Professor não entendi. Explica melhor”.
Poderia responder a dúvida do leitor com meia dúzia de palavras, mas talvez levantasse outras dúvidas, para ele ou para outros.
Às vezes, a dificuldade de se entender alguma coisa está naquilo que chamamos de “falta de base”.
E assim, vou tentar agradar a “gregos e troianos” com esta série de artigos sobre Eletrônica Digital e preparar o terreno para responder a dúvida do Carlos (será que só ele teve dúvida?).
Blá, blá, blá inicial.
Como já foi explicado, no artigo sobre amplificadores digitais, tudo na Natureza é senoidal e, portanto analógico.
Trabalhar com sinais analógicos ficou por conta das primeiras manifestações da eletrônica, ainda no tempo das válvulas, que se convencionou chamar, mais tarde, de “Eletrônica Linear”.
A eletrônica daquela época se preocupava com o áudio e um pouco mais tarde com as telecomunicações que eram chamadas simplesmente de “transmissão”.
Na década de 60 a eletrônica começou a tomar espaço em aplicações industriais e surgiu o que eu chamaria de “primeira manifestação da Eletrônica Digital” com o nome de “Técnicas de Pulsos”.
Meu primeiro livro de “Eletrônica Digital”, em 1967, foi Pulse, Digital and Swtiching Waveforms de Milmman & Taub.
A ideia da Eletrônica Digital ou da “Técnica de Pulsos”, como o próprio nome indica, é trabalhar com “pulsos”, portanto sinais descontínuos, ou melhor, ”discretos” no lugar dos sinais senoidais (contínuos, no sentido de “sem interrupções”).
Esta maneira de trabalhar sinais nos leva a estudar duas coisas que, embora tenham origens distintas acabam se “misturando” :- os circuitos lógicos (apoiado na álgebra booleana) e os números binários.
Bits e Bytes: que “bichos” são esses?
Separar bits e bytes de Informática e Eletrônica Digital é quase impossível. Como dizem por aí, “tá tudo junto e misturado”.
Para entender os tais dos bits e dos bytes, precisamos começar entendendo o que são números binários. Então mãos à obra.
Comecemos pelo significado da palavra bit: binary digit que traduzindo nos dá dígito binário.
E daí? O que é bit ou digito binário?
Uma das definições de bit que aparece no Dicionário de Informática e Internet de Marcia Regina Sawaya é: “um caractere simples em um número binário”
Então, não tem jeito, teremos que estudar os tais números binários.
Sistemas de numeração
O sistema de numeração atual, usado universalmente, é chamado de decimal e tem como base o número 10.
Mas, o que isso tem a ver com a Eletrônica Digital?
No próximo post veremos que a Eletrônica Digital trabalha com o conceito de circuitos lógicos nos quais, diferentemente da Eletrônica Linear, utilizam-se apenas duas condições: ligado (on) e desligado (off).
Para expressarmos matematicamente estes dois “estados lógicos” podemos utilizar os dígitos 0 e 1.
Repare que tive o cuidado de sublinhar a palavra dígito que tem significado diferente da palavra número.
A palavra dígito (que vem de dedo) representa cada símbolo de um determinado sistema de numeração num determinado número.
Assim, o sistema de numeração decimal trabalha com dez dígitos que são: 0, 1, 2, 3, 4, 5, 6, 7, 8 e 9.
O número 10, por exemplo, é então, uma combinação de dois dígitos: o “1” (um) e o “0” (zero).
Coloquei o número 10 como exemplo, mas podemos escrever qualquer número, no sistema decimal, usando apenas os seus dez dígitos (de 0 a 9).
Entretanto, um sistema de numeração capaz de representar circuitos lógicos (ligado e desligado), também “apelidados” de circuitos digitais, só poderá ter dois dígitos e por isso, será chamado de sistema binário (binário significa relativo a dois).
Ora, se o sistema binário só tem dois dígitos quais você escolheria para representa-los?
Acho que não vale a pena querer reinventar a roda numa hora destas. Eu escolheria zero e um e, “por coincidência”, foi isso que os cientistas fizeram!
Então, fica combinado assim, se o circuito está desligado (off) representamos pelo dígito binário 0 (zero), mas se estiver ligado (on) utilizamos o dígito binário 1 (um).
Este será o primeiro ponto onde se apoiará toda a Eletrônica Digital como veremos na parte II.
E o bit, onde entra nesta história?
Lembra-se da definição de bit dada lá atrás: “um caractere simples em um número binário”?
Pois bem, este caractere simples será o zero ou o um, como já vimos.
Aqui, me parece que poderia caber uma pergunta.
Quantos e quais os números decimais poderíamos escrever utilizando os dois bits (0 e 1) do sistema binário?
Veja se concorda com esta resposta: – podemos escrever quatro números decimais usando apenas os dois bits do sistema binário que serão representados por: 00, 01, 10 e 11.
Você saberia dizer quais os números decimais que estes binários representam?
Espero, ansiosamente, que você tenha respondido: 0, 1, 2 e 3.
Sou solidário com você em concordar que, a primeira vista, isto parece um pouco confuso e mal comparando lembra um pouco como aprender a ver horas num relógio “de ponteiro”. Lembra como foi difícil? Mas, você aprendeu não foi! Então, não desanime.
Voltando aos binários você talvez esteja querendo me perguntar: – Como se atreve a dizer que 10 é a mesma coisa que 2 e que 11 vale 3?
Calma que eu explico: – Os “números” 10 e 11 que escrevi no exemplo não estão no sistema decimal e sim no binário. Satisfeito?
Uma coisa e uma coisa, outra coisa é outra coisa!
Você observou que combinando apenas os dois bits (0 e 1) dos binários o máximo de números que conseguimos escrever foi quatro números (00, 01, 10 e 11) o que, convenhamos, não serve para quase nada.
Em outras palavras, com dois bits apenas só obtém quatro valores.
Mas, pensando bem, com os decimais seria a mesma coisa se utilizássemos apenas os seus dez “bits” (ou dígitos) que vão de 0 a 9, nunca iríamos conseguir escrever números maiores que nove.
E aí que os hindus tiveram a grande sacada de “inventar” um sistema de numeração que além de decimal é também posicional, ou seja, cada dígito (de 0 a 9) vai ter um “valor diferente” de acordo com a posição que ocupar no número.
É este sistema decimal posicional que usamos hoje em dia, geralmente, chamado de números arábicos (isso mesmo os hindus inventaram e os árabes levaram a fama).
Por exemplo, no número 2438, o dígito 2 deixa de valer 2 e passa a valer dois mil porque ele está ocupando a posição que chamaremos de “classe” dos milhares.
Da mesma forma, o quatro passa a valer 400 porque sua posição é da classe das centenas. E assim por diante.
Trabalhando com o conceito de base de numeração para simplificar as coisas
Comecemos com a base dez do sistema decimal, uma vez que estamos acostumados com ela desde criancinha.
Entretanto, terei que introduzir algumas ideias que para alguns pode ser novidade, mas acreditem em mim são extremamente importantes para aprender a trabalhar com números binários os quais formam, junto com a álgebra booleana, a base de toda Eletrônica Digital.
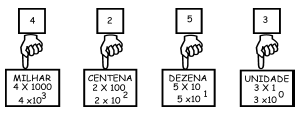
Peguemos, como exemplo, o número 4253 e observe a figura abaixo.
Se estivermos trabalhando no sistema decimal a base de numeração é, obviamente, dez.
Da figura temos:
4253 = 4000 + 200 + 50 + 3 = 4 x 1000 + 2 x 100 + 5 x 10 + 3 x 1 =
A primeira coisa que você precisa observar é que o expoente da base corresponde à classe ao qual o digito pertence.
Vamos destrinchar isso:
1º) Base é 10 porque o sistema de numeração é decimal;
2º) Expoente é o “numerozinho” que está “em cima” da base à
direita e significa que a base deve ser multiplicada por ela
mesma a quantidade de vezes indicada pelo expoente. Por
exemplo, 103 = 10 x 10 x 10.
3º) Expoente 3 que corresponde a classe dos milhares, expoente
2 corresponde a classe das centenas e assim por diante.
4º) A classe das unidades será sempre representada pelo
expoente zero.
Agora vamos fazer a mesma coisa, porém trabalhando com sistema binário no qual a base é dois.
Assim teremos:
Deixo para o leitor a tarefa de continuar até 2 elevado a 12 (se tiver dúvida entre em contato).
Escrevendo números “grandes” em binário
Vimos lá atrás que utilizando apenas dois bits (0 e 1) só poderíamos escrever quatro números binários que correspondem aos decimais 0,1, 2 e 3.
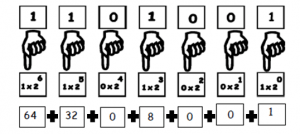
Entretanto, se usarmos nos binários o mesmo conceito de classes que usamos nos decimais poderemos escrever o número que quisermos. Veja o exemplo.
Compare esta figura com a que apresentamos para um número no sistema decimal e observe o que está diferente.
Vou dar uma ajudinha. Basicamente duas coisas estão diferentes:
1º) Em lugar de base 10 temos base 2 (óbvio, o sistema agora é binário);
2º) Os dígitos usados são apenas 0 e 1 que serão chamados de bits.
Assim, no exemplo, podemos concluir que o binário 1 1 0 1 0 0 1 corresponde ao decimal 105 (= 64 + 32 + 8 +1 ).
Reparou que para escrever um “mísero” 105 que no sistema decimal se escreve com apenas três dígitos, no sistema binário precisamos utilizar sete bits.
Já pensou como vai ser para escrever números maiores?
E os bytes, o que são?
Uma palavra muito usada em informática e Eletrônica Digital é o byte, maso que este termo significa afinal?
Quando temos um número binário formado por 4 bits dizemos que ele forma um nibble (leia-se “nibou”).
Por outro lado um número binário formado por 8 bits será chamado byte.
E por falar em byte você seria capaz de dizer qual a maior número decimal que poderíamos escrever com oito bits?
Ora se fizermos os oito bits iguais a um teremos: 1 1 1 1 1 1 1 1 ou
Imagine um número binário composto de 4 bytes, ou seja, 32 bits.
Qual o valor decimal correspondente?
Se você está sofrendo de insônia e contando carneirinhos “binários” para dormir você terá que contar 4.294.967.296 carnei ….. Dormiu?
Na verdade não iremos ficar fazendo estas contas o tempo todo. Isso foi apenas para você perceber que quanto maior o número de bits maior será o valor decimal correspondente que iremos obter.
Grosso modo poderíamos associar os valores decimais ao mundo analógico e os binários ao mundo digital.
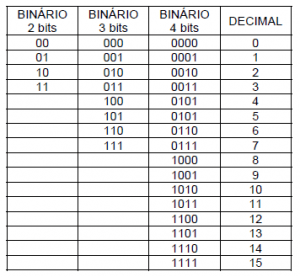
Vejamos isto numa tabela
Na prática chamamos de octal um binário formado por três bits visto que podemos conseguir oito valores decimais (de 0 a 7).
Se trabalharmos com quatro bits poderemos obter 16 valores decimais (de 0 a 15) e neste caso chamaremos de hexadecimal.
Entretanto, quando trabalhamos com quatro bits teremos que arranjar uma maneira “diferente” para escrever os decimais a partir do 9 para que o 1 e 0 de 10, 11, 12, 13, 14 e 15 não seja confundido com os bits 1 e 0 dos binários.
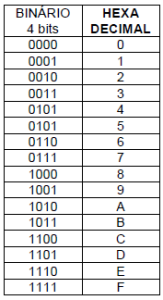
Para resolver esta pequena encrenca adotou-se o uso de letras de A até F para representar estes valores e a tabela dos binários de quatro bits, ou seja, o hexadecimal ficará assim:
Na prática um número binário “muito grande” não costuma ser escrito com todos os seus “1s” e “0s” e sim em arrumando em grupos de 4 em 4 bits.
Por exemplo, o binário de 32 bits 1001 1000 1110 1011 será escrito em forma hexadecimal assumindo o seguinte formato: 9 8 E B.
Vamos ver se você entendeu. Escreva todos os bits (1 e 0) do hexadecimal A 4 3 C (veja a tabela para ajudar).
Se você escreveu 1 0 1 0 0 1 0 0 0 0 1 1 1 1 0 0 parabéns.
No próximo post (vou me esforçar para ele sair quarta-feira próxima) começarei a mostrar como estes binários foram para na eletrônica.
Quem viver verá.
Até sempre.





8 Comentários