E Deus disse “façam-se os bits” e assim surgiu a Eletrônica Digital! – Parte III – Portas Lógicas
No final da parte II eu mencionei que neste post iríamos trabalhar com mais detalhes a álgebra de Boole apresentando as portas lógicas.
Você talvez esteja querendo perguntar: – o que são “portas lógicas”?
Este é um termo bastante usado na Eletrônica Digital que vem do inglês gate(leia-se gueitii) e significa, entre outras coisas, portão ou meio de acesso.
Ainda no posts anterior eu mencionei que a Eletrônica Digital se apoiava na lógica formal por isso, também se diz Lógica Digital ou Circuitos Lógicos.
Naquele momento citei os conceitos de falso e verdadeiro e de proposições lógicas atribuídos a Aristóteles e sistematizados por Boole com sua “álgebra”.
O falso e verdadeiro de Aristóteles virou o 1 e o 0 dos binários que eletronicamente nos deu a “porta” inversora ou NOT.
Uma porta serve para “controlar” a entrada e saída, não é mesmo?
E isso, como já vimos, é o que o circuito inversor faz. Se entrar “verdadeiro” (1) sairá “falso” (0) e vice-versa, se entrar “falso” (0) sairá “verdadeiro” (1).
Para o circuito, os bits 1 e 0 serão níveis de tensão que dependerão da tensão da fonte que o alimenta.
No exemplo mostrado anteriormente o bit 1 correspondeu a 5V porque este era o valor da tensão de alimentação do nosso circuito.
Se tivéssemos trabalhado com 12V, por exemplo, o bit 1 iria valer 12V e bit 0 seria 0V mesmo.
As portas lógicas
Agora vamos tratar das proposições lógicas e das suas “combinações”.
Ainda na parte II, citei o exemplo: – João é brasileiro E João gosta de futebol. Esta proposição é composta de duas proposições simples que estão “ligadas” pelo E (ou AND em inglês) . Acombinação das duas proposiçoes só será VERDADEIRA se cada uma delas em separado for VERDADEIRA.
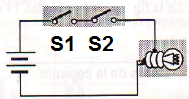
Vamos montar um circuito lógico que represente esta proposição.
Ele terá o aspecto mostrado na figura abaixo.
Consideremos que a proposição “João é brasileiro” seja representada pela chave S1 enquanto “João gosta de futebol” será a chave S2.
A lâmpada que representa a “saída” só acenderá se a chave S1 estiver fechada E a chave S2 também estiver fechada.
Então, se João não é brasileiro, por exemplo, a chave S1 ficará aberta e a proposição composta será falsa o que corresponde a lâmpada ficar apagada.
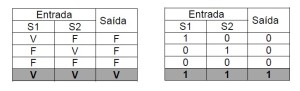
Vamos fazer duas tabelas que representem este circuito lógico para as quatro situações possíveis para cada proposição:
– João é brasileiro (verdadeiro)
– João não é brasileiro (falso)
– João gosta de futebol (verdadeiro)
-João não gosta de futebol (falso)
Numa tabela trabalharemos com os conceitos de Falso e Verdadeiro da lógica aristotélica e na outra com os bits 1 (verdade) e 0 (falso) dos binários. As chaves S1 e S2 serão as entradas e a lâmpada será a saída (essa é função de uma porta, permitir entrar e sair).
Estas tabelas costumam ser chamadas de “tabela verdade” e a deste exemplo corresponde à Porta Lógica AND (“E” em inglês).
Repare que para a proposição composta ser verdadeira é preciso que as duas proposições simples sejam simultaneamente verdadeiras.
Em outras palavras, se João for brasileiro, mas não gostar de futebol a segunda proposição passa a ser falsa o que corresponderia a chave S2 aberta e, portanto a lâmpada não acenderá.
E onde entra a eletrônica?
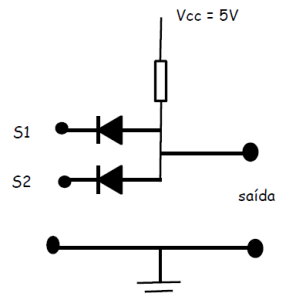
Vamos analisar o circuito abaixo.
As chaves S1 e S2 foram substituídas por dois diodos conforme mostra o circuito acima.
Observe que para a saída ser igual a 1, ou seja, 5V que é a alimentação do circuito, precisamos que as estradas S1 e S2 também estejam com 5V, ou seja, 1(binário), pois aí os dois diodos não conduzirão, já que cátodo e ânodo estarão ambos positivos.
Assim, com esta configuração simples feita com dois diodos acabamos de construir uma porta AND.
E álgebra de Boole?
Boole associou os princípios da lógica aos mesmos princípios utilizados nas operações algébricas básicas como adição e multiplicação.
Ele percebeu que a operação lógica AND correspondia a operação algébrica multiplicação, pois 1 x 1 = 1 enquanto 1 x 0 = 0 x 1 = 0 x 0 = 0.
Usando a linguagem de Boole diremos a saída de uma porta AND só será alta se todas as entradas forem altas. Analise as tabelas verdade e confirme isto.
Onde se usa isto?
As aplicações para uma porta AND são incontáveis e só dependerão da imaginação e necessidade do projetista.
Por exemplo, para uma impressora começar a imprimir ela precisa ter papel na bandeja e reconhecer que há cartucho instalado.
Estes pontos serão monitorados por sensores e ambos terão que enviar nível lógico alto a uma porta AND dentro do processador que permitirá que a impressão seja iniciada.
Citei uma impressora como exemplo, mas poderia ser qualquer outro equipamento.
Nem sempre a porta está embutida dentro de um processador. Ela pode ser feita externamente e sua saída levada ao processador ou outro circuito qualquer.
Existem outras portas além da porta AND?
Sim, existem.
Deixarei para tratar delas no próximo post para não “fundir a sua cuca”.
Quero ver também como foi absorvido o assunto deste post. Aguardo comentários e sugestões.
Ah! Ia esquecendo, próximo sábado, 17 de maio, o meu amigo Fernando do José do Clube do Técnico-RJ irá realizar mais um dos seus treinamentos de atualização para técnicos de TV.
Até sempre.