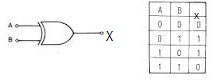E Deus disse “façam-se os bits” e assim surgiu a Eletrônica Digital! – Parte IV – Portas Lógicas – continuação
No final do post anterior apresentei a porta AND e sua respectiva tabela verdade.
Uma das coisas interessantes da Eletrônica Digital e que, a meu ver, torna-a até mais fácil de estudá-la em comparação com a Eletrônica Linear é que, na maioria das vezes, não iremos trabalhar com componentes discretos como na porta AND feita com diodos.
No primeiro momento talvez você queira me contestar quando digo que a Eletrônica Digital é mais fácil que a Linear, mas ao longo desta série de artigos vou lhe provar que o que digo é verdade.
Símbolo da porta AND e tabela verdade
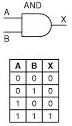
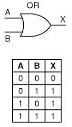
Na Eletrônica Digital trabalharemos com blocos lógicos. Por exemplo, uma porta AND de duas entradas será representada simplesmente pelo símbolo ao lado. Junto está a sua tabela verdade.
Você não precisa saber o que tem dentro da “caixa preta” representa pelo símbolo nem tão pouco como o circuito que está lá dentro funciona.
Basta você saber que:
A SAÍDA DE UMA PORTA AND SÓ SERÁ ALTA (BIT 1) SE TODAS AS ENTRADAS FOREM ALTAS.
Repare que eu disse “todas as entradas”, mas no nosso exemplo o “todas” é igual a duas entradas que denominamos A e B.
Simbolo da porta AND de 3 entrdas
E se fossem três entradas (A, B e C)?
Neste caso nossa tabela verdade será a mostrada acima.
Note que a saída só é alta quando todas as entradas são altas (última linha da tabela).
Como isto funciona na prática?
Do ponto de vista da reparação, se você encontra a saída de uma porta AND com 0V, ou seja, em nível lógico baixo é porque pelo menos uma de suas entradas está em 0V (nível baixo).
O que se deverá fazer a seguir é verificar cada uma das entradas (2, 3 ou quantas forem) e se constatar que todas estão em nível alto (5V, por exemplo) você acabou de descobrir que esta porta está defeituosa ou há algum componente “pendurado” em sua saída que está em curto.
Viu como é simples. Você não precisa ficar testando transistores um a um como num circuito linear.
Mais portas lógicas
Relembremos as duas proposições simples, apresentadas na parte III:
– João é brasileiro
– João gosta de futebol.
Naquele momento construímos uma proposição composta utilizando o E para “juntar” as duas: João é brasileiro E João gosta de futebol.
Agora, vamos “juntar” as duas proposições simples utilizando o OU no lugar do E. Teremos então João é brasileiro OU João gosta de futebol.
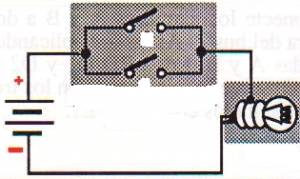
Vamos representar esta proposição composta que receberá o nome de porta OU (OR em inglês) por um circuito com duas chaves do mesmo modo que fizemos com a porta AND só que agora as chaves estarão em paralelo e não em série como no caso da porta AND.
Repare que neste caso para proposição ser verdadeira, ou seja, para a lâmpada acender, basta que pelo menos uma das chaves S1 ou S2 estejam ligadas.
Construção de uma porta OR com chaves
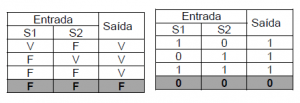
Da mesma forma que fizemos com o AND vamos construir duas tabelas verdade para a porta OR. Numa utilizaremos o conceito de Verdadeiro e Falso de Aristóteles e na outra o conceito de bits 1 e 0 da álgebra de Boole.
Tabela verdade d porta OR
Observe que no caso da porta OR:
A SAÍDA SERÁ BAIXA SE TODAS AS ENTRADAS FOREM BAIXAS.
Esta porta corresponde a adição, ou seja, 1 + 0 = 1, 0 + 1 = 1, 0 + 0 = 0 e, finalmente 1 + 1 = 1.
Ops! Que história é essa de 1 + 1 = 1. Sempre me ensinaram que 1 + 1 = 2.
Calma! Lembre-se que estamos trabalhando com números binários e, portanto o “símbolo” 2 não existe. Nos binários só temos 0 e 1.
Quando somamos 1 + 1 em binário dá 0 “e vai um” para a classe superior, da mesma forma como acontece nos número decimais. Se somarmos 9 + 1 dá 0 “e vai 1” por isso, é que escrevemos 10. Lembre-se que nos decimais não existe o algarismo 10, somente os algarismos de 1 a 9.
Construindo uma porta OR com diodos
Porta OR de 2 entradas com diodos
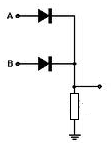
Do mesmo jeito que fizemos com a porta AND vamos dar um “toque” de eletrônica e construir uma porta OR com diodos no lugar das chaves.
Observe que a saída só será baixa se as duas entradas estiverem em nível baixo mantendo os diodos cortados.
Simbologia da porta OR
Símbolo da porta OR e tabela verdade
Da mesma forma que fizemos com a porta AND não utilizaremos um circuito com componentes discretos para representar a porta OR e sim o símbolo mostrado ao lado junto com sua respectiva tabela verdade.
Negando tudo
Até aqui já construímos três portas lógicas, a saber, a porta inversora ou NOT, a porta AND e a porta OR.
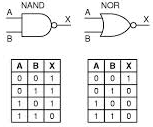
Podemos associar a porta NOT às portas AND e OR e obter duas novas portas que serão chamadas respectivamente de NAND e NOR.
Sempre que quisermos representar a negação, ou seja, a inversão de uma porta colocaremos uma “bolinha” no terminal correspondente. Veja abaixo como ficarão os símbolos das portas NAND e NOR e suas respectivas tabelas verdade.
Símbolos das portas NAND e NOR e tabelas verdade
Ainda falta uma porta
Para finalizar este estudo das portas lógicas ainda precisamos acrescentar mais uma, ou melhor, duas. A porta chamada OU EXCLUSIVO e sua negação.
Aqui cabe fazer algumas observações “linguísticas”, digamos assim.
Consideremos a proposição composta “vou à praia OU ao teatro”.
Do ponto de vista da nossa “maneira de falar” popularmente esta proposição costuma ser interpretada que “ir à praia” exclui a ideia de “ir ao teatro” ou vice-versa.
Entretanto, se usarmos a tabela verdade da porta OR (ou) estudada anteriormente veremos que há a possibilidade de “irmos” aos dois lugares (praia e teatro).
Em outras palavras, a tabela verdade da porta OR na verdade funciona como e/ou, isto é, três condições são verdadeiras:
– ir à praia
– ir ao teatro
– ir à praia E ir ao teatro.
Observe a tabela verdade e note que a proposição só será falsa se o declarante “não for à praia e não for ao teatro”.
Símbolo da porta Exclusive OR e tabela verdade
Mas o objetivo da lógica é não deixar dúvida e contemplar todas as possibilidades de pensamento, sendo assim criou-se uma porta denominada EXCLUSIVE OR (ou exclusivo), também denominada XOR cujo símbolo e tabela verdade vemos ao lado.
Esta porta é sem dúvida, talvez a mais difícil de ser entendida, por isso vou deixar para o próximo post a apresentação de um circuito que a represente.
Finalmente podemos também negar a porta XOR assim como fizemos com as demais e obter a porta XNOR (não vá confundir com caldo Knorr!).
Mas isto, como já disse, fica para o próximo post.
Até sempre.
