Entendendo os valores dos capacitores
Entendendo os valores dos capacitores
 Decidi escrever sobre os valores dos capacitores (ou condensadores como dizem os “antigos” e os espanhóis) por causa de um pedido de alguém que apareceu num destes grupos do facebook.
Decidi escrever sobre os valores dos capacitores (ou condensadores como dizem os “antigos” e os espanhóis) por causa de um pedido de alguém que apareceu num destes grupos do facebook.
O participante do grupo estava à cata de um capacitor cerâmico de “1,2nF” e dizia não encontrar em lugar nenhum.
A primeira questão é que ele não mencionava a tensão de trabalho do capacitor o que realmente poderia se um complicador caso fosse um capacitor para tensão alta como 1 ou 2kV.
Ora, os veteranos sabem que este valor de capacitor (se não for para alta tensão) é bastante comum e não é deve ser difícil de conseguir, entretanto muita gente dava palpites, mas ninguém ajudada o “pobre coitado”.
Resolvi entrar na brincadeira e para não ficar no bate boca ali no face pedi-lhe que entrasse em contato comigo por e-mail.
Pouco a pouco fui descobrindo que ele era um hobbista e que quase não tinha conhecimento do assunto.
Não vejo nenhum problema nisto, pois não sou preconceituoso e acho que montar “circuitinhos” pode ser uma boa “porta” para entrar no mundo da Eletrônica, então resolvi ajudá-lo.
Resumo da ópera: mandei-lhe um capacitor pelo correio para ele montar um micro transmissor de FM achado na Internet e agora sim vamos ao assunto do post.
O passado no presente (Como diz o meu amigo Jaime no seu grupo do facebook sobre a Ilha do Governador)
Quando eu comecei na Eletrônica lá pelos idos de 1960 (naquela época chamava-se Rádio Técnico) não se expressavam os valores de capacitores em “nano farads” ou “pico farads” como hoje.
Os valores eram escritos em “microfarads” e era comum ver-se nos esquemas coisas como: .05 MF ou .0002 MF e por aí vai.
A nomenclatura de componentes eletrônicos era (quase) toda americana, por isso o “ponto” no lugar da vírgula que é o padrão deles. Para “simplificar” a escrita o zero antes do ponto era omitido e o M representava ERRADAMENTE o submúltiplo “micro” que deveria ser simbolizado pela letra grega “μ” (leia-se “mi”).
O tempo foi passando, a eletrônica se popularizou e deixou de ser um “monopólio” dos americanos (o “monopólio” passou para os japoneses e atualmente está com os chineses).
Por outro lado, os componentes, entre eles os capacitores, foram cada vez diminuindo mais de tamanho e começou a faltar espaço para escrever coisas como “.0005MF” no corpo do capacitor.
E foi aí que entraram em cena o “nano e o pico” e algumas formas “diferentes” de se escrever os valores dos capacitores quer no componente em si, quer no esquema.
Um pouco de matemática numa hora dessas não faz mal a ninguém!
Creio que a principal complicação em entender os valores dos capacitores pode estar principalmente em dois pontos:
1) A unidade de capacitância, o farad (homenagem a Michael Faraday) cujo símbolo no Sistema Internacional (SI) é o F maiúsculo é, por definição, uma unidade muito grande o que obriga, na prática, a trabalharmos com submúltiplos do farad. Em outras palavras, na prática não se usam capacitores com valores em farads. Só encontramos isso nos problemas dos livros de física!
2) A maioria das pessoas tem dificuldades em trabalhar com números muito pequenos, ou seja, números do tipo 0,00000000xxxxx porque não aprenderam muito bem isso na escola (ou foi mal ensinado).
Sendo assim, é melhor começar pelo começo.
O que são múltiplos e submúltiplos ou como não escrever tantos zeros?
De maneira bem simples podemos dizer que um múltiplo é um valor que multiplica alguma coisa, portanto seguindo este “raciocínio” um submúltiplo deve dividir.
Ficou confuso?
Quando você vai ao mercado e compra, por exemplo, “um kilo” de feijão você está comprando “um quilograma” de feijão ou “mil gramas” de feijão.
Se você é um bom observador e na infância brincou com o joguinho dos sete erros, deve notado duas coisas no parágrafo acima.
A primeira delas é que num momento eu escrevi “kilo” com “k” e no outro com “q-u-i” e a segunda é que a “palavra” kilo ou quilo foi substituída por mil.
Antes de passar adiante vamos logo esclarecer isto. A palavra “kilo” (com k) vem do grego khilioi e significa mil, entretanto no alfabeto da língua portuguesa não existe a letra “k”, por isso a forma correta de se escrever “kilo”, no Brasil, é “quilo” (como disse um político brasileiro “fi-lo porque qui-lo” kkk).
A segunda observação é que “kilo” ou “quilo” que significa mil se simboliza internacionalmente pela letra “k” minúscula, daí quando escrevemos 1kg estamos querendo dizer “mil gramas”.
Da mesma forma quando escrevemos “1km” estamos querendo dizer “um quilômetro ou mil metros” ou “1kohm” é o mesmo que “mil ohms” e por aí vai.
Feita esta pequena digressão de capacitor para feijão, voltemos ao objetivo deste parágrafo que é explicar o que são múltiplos e submúltiplos.
Para evitar que se tenham que escrever tantos zeros antes ou depois do primeiro algarismo significativo adotou-se internacionalmente símbolos através de letras para “substituir” os zeros. Um deles, acabamos de ver é a letra “k” que corresponde a mil (1000) e é bastante usado como acabamos de ver.
Outros múltiplos bastante usados na prática são:
1) mega = 1.000.000 (um milhão) que simbolizamos por M maiúsculo. Por exemplo, velocidade da Internet 10Mb/s significa “dez mega bytes por segundo” (você paga por 10, mas não recebe 10!). Ah! NUNCA diga “coisas” do tipo dez megaS.
2) giga = 1.000.000.000 (um bilhão) que simbolizamos por G maiúsculo. Por exemplo, memória de 2GB significa “dois giga bytes”. Aqui também não se diz gigaS.
3) tera = 1.000.000.000.000 (um trilhão) que simbolizamos por T maiúsculo. Por exemplo, HD de 2TB ou “dois tera bytes”.
No caso da Eletrônica usamos, em geral, apenas o quilo (k) e o mega (M) quando nos referimos a resistências ou tensões.
Agora passemos aos submúltiplos que são utilizados nos capacitores.
1) mili = 0,001 (um milésimo) que simbolizamos pela letra “m” minúscula. Este é um caso especial, pois o “m” minúsculo tanto pode ser submúltiplo como o símbolo de metro daí que milímetro seja expresso por “mm”. Na Eletrônica o “mili” costuma ser usado em valores de tensões muito baixas como, por exemplo, 5mV que é o mesmo que 5 milivlots ou 0,005V.
2) micro = 0,000 001 (um milionésimo). Embora micro também comece com a letra m para evitar mais uma confusão foi adotada a letra grega “mi” (μ) para simbolizar o micro. Por exemplo, 10μF significa “dez microfarads”, ou seja, o mesmo que 0, 000 001F.
3) nano = 0, 000 000 001 (um bilionésimo). O nano é simbolizado pela letra “n” minúscula e aí em vez de escrever”.000 000 001F” escreve-se 1nF. Então o capacitor procurado de 1,2nF seria escrito na “moda antiga” como “.000 000 001 2F”. Haja zero antes do 1, parece o saldo da nossa conta bancária no final do mês (ou antes)!
4) pico = 0,000 000 000 001 (um trilhionésimo). O pico é simbolizado pela letra p minúscula. Na Eletrônica “antiga” ainda no tempo das válvulas não era muito como usar-se capacitores de picofarads, por isso este números raramente apareciam.
Outras formas de escrever os valores dos capacitores
Uma forma que costuma ser usada para escrever os valores dos capacitores, principalmente nos esquemas é “substituir” a vírgula (ou ponto) pela letra que representa o símbolo do submúltiplo.
Nada melhor que um exemplo para esclarecer. O capacitor de 1,2nF do hobbista pode ser escrito também como “1n2” onde o F de farad foi sumáriamente omitido, já que se este valor estiver ao lado do símbolo de uma capacitor ou no próprio corpo da peça, fica subentendido que só pode ser F. E tem mais, na prática fala-se “um nano dois” e estamos conversados!
Transformando nano em pico e vice-versa
Outra coisa que costuma confundir a cabeça dos técnicos até mesmo veteranos é que este mesmo capacitor “1n2” pode ser representado também por 1200pF.
Esta “metamorfose” nos números é um pouquinho mais difícil de entender, mas não é nenhum bicho de sete cabeças.
Você reparou que um nano é mil vezes maior que um pico?
Tá confuso? Então olha só
1 nano = 0,000 000 001 (9 zeros antes do 1)
1 pico = 0,000 000 000 001 (12 zeros antes do 1)
A diferença entre o nano e o pico é que o pico tem três zeros a mais antes do 1 que o nano.
Logo se eu quiser transformar nano em pico eu coloco estes três zeros depois do 1 e então, 1 nano = 1.000 pico que também pode ser escrito como “1kpF” substituindo-se o 1000 pela letra k (minúscula). Em outras palavras eu tenho que multiplicar o valor em nano por 1000 para que ele “vire” pico.
Vamos ver se você entendeu. Um capacitor de 4,7nF é igual a um capacitor de …….. pF.
Se você colocou 4700 no lugar dos pontinhos acima, parabéns!
Como eu cheguei aos 4700? Simples multiplicando 4,7 por 1000.
Mas também poderia ser escrito 4,7kpF ou, mais comumente, 4K7pF.
Lembra que eu disse que a vírgula costuma ser substituída pela letra k que representa o múltiplo?
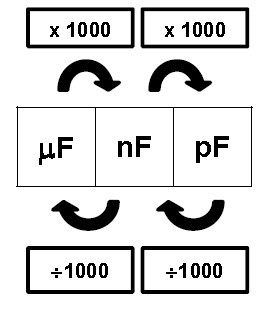
Uma tabelinha para ajudar a simplificar as contas
Por exemplo, para passar .002 μF para nanofarad multiplicamos por 1000 o que nos dá 2nF. Para passar para nanofarad multiplicamos por 1000 novamente e obteremos 2000pF ou 2kpF.
Dever de casa
A melhor ou a única maneira de se aprender alguma coisa é fazendo, então mão a obra.
1) .0015μF = _______ nF = _______ pF
2) .00047μF = _______nF = _______ pF
3) .1μF = _______ nF = _______ pF
4) 470 nF = _______ μF = _______ pF
5) 220kpF = _______ μF = _______ nF
Por enquanto é só. Manda as respostas para contato@paulobrites que eu digo se você acertou.
Até sempre




16 Comentários