Leis de Kirchhoff e Sistemas de Equações Lineares
Leis de Kirchhoff e Sistemas de Equações Lineares
Malha resistiva
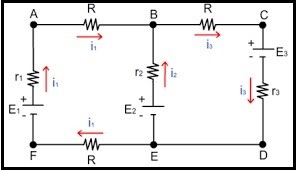
Um dos tópicos de eletricidade que costuma causar pânico aos estudantes e que, quase sempre, aparece nas provas de concursos, são os circuitos elétricos envolvendo resistores e fontes de tensão como o da figura ao lado.
Vários são os métodos para resolução destes circuitos e um deles, que servirá de “gancho” para este post, utiliza as Leis de Kirchhoff.
Na verdade não irei tratar do método de Kirchhoff propriamente para obter o sistema de equações lineares dele decorrente e que nos permitirá encontrar as correntes no circuito, o que me interessa mesmo é mostrar como se pode simplificar a resolução dos sistemas de equações lineares quando temos três ou mais equações.
Vale lembrar que o que vai ser apresentado aqui, obviamente, não se aplica apenas ao caso particular das malhas de Kirchhoff e pode ser utilizado em que qualquer situação que se necessite resolver sistemas de equações lineares.
Quando o sistema tem apenas duas equações e duas incógnitas a sua resolução é bem simples, podendo se utilizar os chamados métodos de adição ou substituição, e por isso a “mágica” que eu vou apresentar não vale muito a pena nestes casos.
O que interessa mesmo é simplificar a resolução de sistemas com três equações e três incógnitas ou mais.
Os livros de matemática costumam recomendar o uso de determinantes da matriz obtida a partir do sistema, um pouco trabalhoso, mas atende a quem é afeito a decorebas.
O bicho pega mesmo é a partir de quatro equações e quatro incógnitas e no meio de tantas regrinhas de simplificação de determinantes o estudante acaba “entrando em curto”.
O fabuloso “método” de Gauss
Aprendi a resolver sistemas de equações lineares por este método, que tecnicamente é o que se chama em matemática de algoritmo, através do meu inesquecível professor Paulo Baptista de Oliveira, o PBO, lá no meu curso técnico.
Nunca o tinha visto antes e confesso que nunca vi, até hoje, nenhum livro explicando-o.
Por que será que não ensinam coisas úteis e práticas?
Nas linhas a seguir vou apresentar o passo a passo para resolução de um sistema com quatro equações e quatro incógnitas aqui designadas por i1 até i4 porque surgiram da aplicação das Leis de Kirchhoff em algum circuito (não o do exemplo dado) que não interessa aqui mostrar.
Se você é um estudante de ensino médio ou está tentando resolver sistemas deste tipo, comuns também em álgebra linear, as letras i1 até i4 aparecerão como x, y, w e z. Dá no mesmo.
Vamos a um exemplo.
Suponhamos que ao analisar uma malha resistiva de um circuito, Kirchhoff nos deu as seguintes equações:
i1 – 2 i2 = 3 i3 – 4i4 – 4
3 i1 – i3 + 2 i4 – 16 = 0
5 i2 + 2 i3 = 3 i4 + 20
i2 – 7 i4 – 10 = – i2 – 4 i1
Para aplicar o método devemos seguir os três passos abaixo.
Arrume o sistema da seguinte maneira:
- Coloque todos os termos que possuem as incógnitas do lado esquerdo do sinal de igualdade e os termos constantes do lado direito;
- Faça a arrumação de modo que as mesmas incógnitas fiquem alinhadas na mesma coluna;
- Se faltar uma incógnita complete sua coluna com coeficiente zero e se “não tiver” coeficiente, significa que é um.
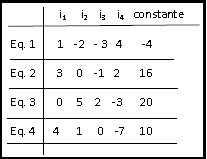
1 i1 – 2 i2 – 3 i3 + 4i4 = – 4 equação 1
3 i1 + 0 i2 – 1 i3 + 2 i4 = 16 equação 2
0 i1 + 5 i2 + 2 i3 – 3 i4 = 20 equação 3
4 i1 + 1 i2 + 0 i3 – 7 i4 = 10 equação 4
Até aqui nada de novo. Seja lá o método que se queira utilizar, esta arrumação “na casa” é sempre muito útil.
Lembre-se: – a organização é metade da execução!
Uma vez arrumado todo o sistema construa o seguinte quadro:
Arrumando um sistema de equações lineares
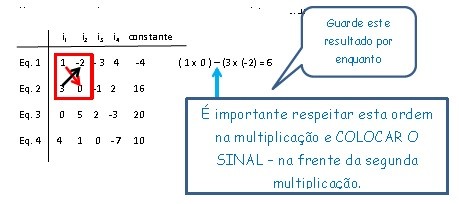
Uma vez montado o quadro acima (que repito abaixo) faça as operações mostradas a seguir considerando SEMPRE as linhas e colunas da Eq.1 como referência.
Algoritmo para resolver um sistema de equações lineares
Repare que no primeiro cálculo trabalhamos com a primeira e a segunda linha, bem como primeira e segunda coluna.
Veja no destaque abaixo.
Começando a usar o algorímo
Vamos passar para o próximo cálculo e você já vai pegar o jeito.
Efetuando o segundo cálculo
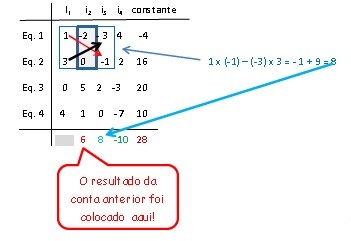
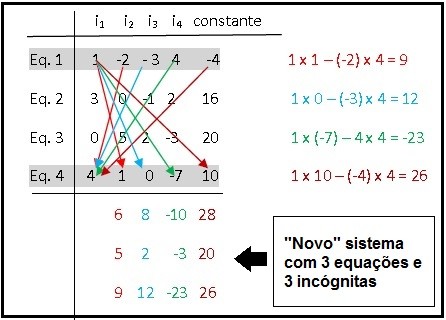
Repare na figura acima que agora eu “pulei” a segunda coluna e trabalhei com a primeira e a terceira colunas.
Repare onde foi colocado o “6” do cálculo anterior.
Criei uma nova linha abaixo da Eq.4, mas sem a primeira coluna e “8” da conta da segunda conta, agora foi colocado ao lado do “6”.
Você seria capaz de descobrir como surgiu o “-10” que aparece do lado do “8”?
É assim, “pulei a segunda e terceira coluna e trabalhei com a primeira e quarta: 1 x 2 – 4 x 3 = 2 – 12 = – 10.
E o 28? Experimente fazer primeira coluna com a quinta:
1 x 16 – (3 x (-4)) = 16 + 12 = 28.
Com este procedimento “elimina-se” a primeira coluna.
O próximo passo será fazer cálculos parecidos, mas trabalhando com a primeira e terceira linha do sistema original. Veja a figura.
Já desconfiou o que vem a seguir? Será trabalhar com a primei4a e quarta colunas e o resultado fica do jeito mostrado abaixo.
Sistema reduzido de 4 para 3 equações
Reparou que nosso sistema foi reduzido de quatro equações com quatro incógnitas para um “novo” sistema de três equações com três incógnitas e só tivemos trabalho “braçal” para fazer isso. Não precisamos “pensar”!
E agora, se aplicarmos o método ao “novo” sistema “três por três” dá pra desconfiar que obteremos um sistema “dois por dois”?
Em outras palavras, a ideia é ir reduzindo o número de equações e o número de incógnitas até chegar a uma equação com uma incógnita.
Veja como vai ficar.
Encontrando a primeira incógnita
Acabamos de descobrir o valor de i4.
Se você olhar as equações 8 e 9 do quadro acima verá que só temos i3 e i4 e o valor desta última já sabemos que é igual a 2.
Antes, porém vale a pena observar que neste caso podemos dividir por quatro todos os números da eq.8 e assim, teremos números menores o que, sem dúvida, facilita as contas.
A equação 8, após a simplificação, nos dá -7 i3 + 8 i4 = -5 e portanto, se substituirmos i4 por 2 teremos
– 7 i3 + 8 x 2 = -5 ou finalmente i3 = 3.
Pronto já encontramos o valor de mais uma incógnita, i3. A fila está andando!
Já desconfiou qual será o próximo passo?
Espero que tenha dito que é encontrar o valor de i2 e para tal vou escolher as equações 5, 6 ou 7.
Aí fica a gosto do freguês, se tiver uma “mais barata”, isto é, com números menores, vamos nessa.
Neste caso parece que tanto faz, então vou pegar a equação 5 mesmo: 6 i2 + 8 i3 – 10 i4 = 28 e fazer i3 = 3 e i4 = 2.
Vamos às contas: 6 i2 + 8×3 – 10×2 = 28 o que nos dará i2 = 4.
“Matamos” mais uma incógnita e só falta i1.
Podemos escolher qualquer uma das quatro equações originais e substituir os valores já “descobertos” de i2, i3 e i4 para achar i1.
Uni, dune, tê, eq.1 a escolhida foi vo….CÊ.
E a luta continua: i1 -2 x 4 – 3 x 3 + 4 x 2 = -4 e tchan, tchan, tchan … i1 = 5.
Gostou, então vou deixar um sistema para você praticar e postar as respostas nos comentários.
x – 2 y – 3 z + 4 w + 4 = 0
3 x + 2 w – z – 16 = 0
-3 w + 5 y +2 z = 20
4 x – 7 w + y = 10
Divirta-se, vai ser emocionante!
4 Comentários