Logaritmos e eletrônica
Logaritmos e eletrônica
Parte I
Se o título, logaritmos e eletrônica, deixou você curioso ou confuso, era isto que eu queria aliás, não são só os logaritmos e a eletrônica que estão conectados, a música, os juros, os terremotos e muitas outras “coisas”
Leia até o fim e você chegará a uma conclusão interessante: tudo no mundo está conectado de alguma forma e o elo desta conexão é a matemática.
Como eu sempre repito, Galileu dizia “a matemática é a linguagem que Deus usou para descrever o Universo”.
Não precisa suar frio só porque eu mencionei a palavra matemática. Continue lendo, “pelo amor de Deus” e talvez que você seja surpreendido com que vem por pela frente.
Este artigo, que não é só sobre logaritmos e eletrônica, estava engavetado (ou “hdsado”) há muito tempo, mas meu perfeccionismo sempre achava que não estava bom e eu ia adiando a sua publicação, até que chegou a hora.
Finalmente me rendi ao ditado que diz “melhor feito do que bem feito” e resolvi deixá-lo sair do ”barril de carvalho”, mesmo antes dos 12 anos de envelhecimento, para “degustação” dos leitores.
O que ouvimos por aí.
Os noticiários anunciaram que o tremor teve magnitude de 8,4 na escala Ritcher. E daí? Você sabe o que é isto quer dizer? É muito ou pouco?
O som estava a mais de 80 dBs, dizia a reportagem.
E os juros? Bem estes estão nas nuvens (no Brasil) e os banqueiros agradecem.
Você vai comprar um potenciômetro, chega à loja pede “um potenciômetro de 100K” e o balconista pergunta: linear ou log.
Pra não passar por ignorante você faz cara paisagem e responde: hummm! Linear. Bem, se era para ser usado como controle de volume do amplificador vai “dar ruim”, como dizem por aí.
Estes são alguns exemplos de “coisas” aparentemente desconectas, mas que no fundo se conectam e a conexão está num conceito chamado logaritmo “inventado” lá pelo século XVI, por três sujeitos ao mesmo tempo e que não se conheciam, moravam muito distante um do outro e lembre-se que era século XVI e a Internet não existia nem tão pouco o Google!
Brincando com números
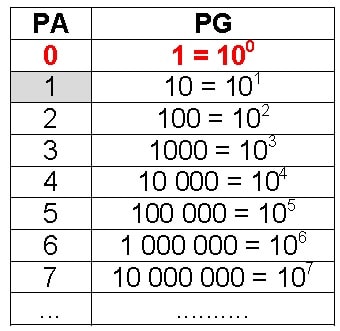
Comecemos examinando as duas sequências numéricas abaixo:
Tabela de PA e PG
Elas poderiam seguir indefinidamente, mas com estes valores já podemos tirar algumas conclusões.
Observe que a sequência da esquerda começa com o número zero e cada número seguinte é obtido somando-se um ao anterior. Já a sequência da direita começa com o número um e cada número seguinte é obtido multiplicando-se o anterior por dez.
Os matemáticos chamam a sequência da esquerda de progressão aritmética (PA) e a da direita é chamada de progressão geométrica (PG). Então, daqui por diante vou me referir sempre a PA e PG.
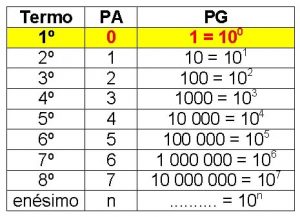
Além disso, cada número da sequência será chamado de termo da progressão seja ela aritmética ou geométrica.
Por exemplo, da nossa primeira tabela o número 1000 é o quarto termo da PG, enquanto na PA o quarto termo é o número 3.
Tá confuso? Vou esclarecer.
Isso acontece porque a PA começa em zero, enquanto a PG começa em um. Isto não precisa ser sempre assim, mas para “inventarmos” os logaritmos será melhor fazer desse jeito.
Tabela I – relacionando PA e PG
Outra coisa que é bom saber, para facilitar nossa conversa daqui pra frente, é que o número que devemos usar para somar a um termo da PA a fim de obter o termo seguinte costuma ser chamado de razão da PA. No nosso exemplo tabela I a razão da PA é igual a um.
Poderíamos utilizar qualquer outro valor diferente de um para a razão da PA, entretanto esta escolha facilitará a nossa “invenção”, ou melhor, a invenção dos senhores Briggs e Napier.
Da mesma forma a razão de uma PG é o número que multiplicamos um termo para obter o termo seguinte.
Observe que no nosso caso na tabela I a razão da PG é 10.
Ainda nesta tabela vemos que os termos da PG foram escritos de duas maneiras que são equivalentes. O número “completo” com todos os zeros ou em forma de potência onde a base é 10 (que neste exemplo é a razão da PG) e o expoente por “coincidência” é o termo correspondente da PA. Por exemplo, 100 000 = 105.
Tabela I com destaque para o 6º termo
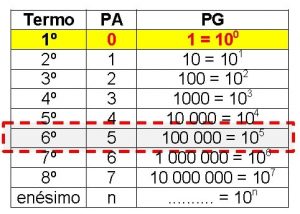
Agora imagine que você queira multiplicar 100 por 10.000. Em vez de fazer a multiplicação observemos que o 100 da PG corresponde ao 2 da PA e 10.000 corresponde ao 4. Se nós somamos 2 + 4 obteremos 6. Note que o 6 da PA corresponde a 1.000.000 na PG que é exatamente o resultado da multiplicação de 100 por 10.000.
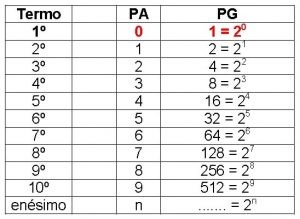
Eu escolhi o 10 como razão da PG para facilitar, mas, como já disse antes, poderia ser outro número qualquer, por exemplo, 2.
Acompanhe na tabela II
Tabela II – Razão da PG igual a 2
Neste caso, multiplicar 4 por 32 (=128), por exemplo, corresponde a somar 2 + 5 = 7.
Muito bem, esta “matemágica” permitiu que “transformássemos” multiplicações em somas e, diga-se de passagem, que, sem dúvida, somar é muito mais “fácil” que multiplicar.
Espero que você tenha percebido que poderíamos também “transformar” divisões em subtrações ou no popular, “conta de menos”.
Por exemplo, dividir 1 000 000 por 100 seria o mesmo que subtrair 6 de 2 que dá 4 e na tabela I corresponde a 10 000. Confira e comprove. Ou ainda dividir 512 por 8 seria subtrair 3 de 9 que nos dá 6 na coluna da PA e corresponde a 64 na coluna da PG. É só conferir na tabela II.
Você certamente está pensando em argumentar “não é mais fácil usar uma calculadora para fazer multiplicações ou divisões?”.
Concordo plenamente, mas agora vamos entrar no túnel do tempo e voltar para 1614.
Alguém aí tem uma calculadora pra me emprestar que eu tenho que fazer umas multiplicaçõezinhas e divisõezinhas aqui?
Hein! Cal… o quê?
Um pouco de história
Pois é, foi diante deste problema que lá por 1600 e antigamente um relojoeiro suíço chamado Jost Bürgi “inventou” este método de fazer multiplicações através de somas.
Só que ele não publicou suas ideias e aí um escocês chamado John Napier (que não era matemático) teve outra ideia, mas com o mesmo objetivo e publicou, em 1614, um livro com tabelas para transformar multiplicações em somas que ele denominou Logarithmorum Canonis Descriptio.
A ideia de Napier teve apoio imediato e entusiástico de Henry Briggs que era professor de geometria em Oxford.
Em 1615, Briggs visitou Napier e propôs uma modificação no seu método para que utilizasse potências de dez em vez do valor (1-10-7) que ele usava. A proposta foi aceita.
Claro que não eram as continhas tão simples como as do exemplo, mas a ideia, em síntese, é a mesma.
Uma observação que você talvez queira fazer é que o método só trata de números inteiros e se quiséssemos multiplicar coisas como 14598 por 23879, por exemplo.
Briggs percebeu isso e muito mais. Ele notou que se construísse uma tabela com o maior número possível de valores entre 1 e 9, seria suficiente para fazer qualquer conta de multiplicar.
Ele trabalhou duro nesta tabela por vários anos num processo de extração de raízes que não tratarei aqui porque foge um pouco ao meu objetivo principal.
E assim nasceu o logarítmo
Como já vimos os termos da PA são os expoentes que aparecem nos termos da PG. Inicialmente Napier chamou estes expoentes de “números artificiais”.
Mais tarde Napier “inventou” a palavra logaritmo (que passou a usar no lugar de números artificiais) juntando as palavras gregas logos que significa razão ou proporção com aritmos que significa números e assim, Napier ficou sendo considerado o “pai” dos logaritmos (ninguém sabe quem é a mãe).
Se fizermos a diferenças entre dois logaritmos quaisquer (que são dois termos da PA ou expoentes dos termos da PG), por exemplo, 7 – 3 veremos que o resultado 4, neste caso, corresponde a divisão (razão) entre 10.000.000 e 1000 que é 10.000 cujo logaritmo é realmente 4.
Conclusão, a invenção de Bürgi e Napier e o aprimoramento e dedicação de Briggs servia para “transformar” multiplicações e divisões em somas e subtrações o que, convenhamos, simplificava muito a vida de quem tina que fazer muitas contas naquela época como os astrônomos (não confundir com astrólogos, por favor) e navegadores.
Mais tarde veremos que será de grande utilidade também para resolver problemas de radiciação.
Como se ensina logaritmo na escola
Nos livros de ensino médio, em geral, os logaritmos são apresentados de uma forma que eu diria quase “brutal” sem mostrar ao aluno qual a motivação que levou a sua invenção (eu também já ensinei assim).
Sou um fervoroso adepto que não só a matemática, mas também a física seja apresentada aos alunos através do que eu chamo de “uma caminhada histórica” e na física não se deve desprezar o lado experimental em favor da simples matematização como normalmente é feito.
As matemáticas surgem da resolução de algum problema da vida prática. Em outras palavras, ninguém acorda um dia e diz “hoje eu vou inventar uma nova matemática porque estou a fim de fazer os alunos se ferrarem na prova”.
A definição de logaritmo que aparece em quase todos os livros é, mais ou menos, assim:
Definição algébrica de logaritmos
Então, por exemplo, logaritmo de 100 na base 10 é igual a 2 ou, simplificadamente Log10 100 = 2. Pra simplificar ainda mais a nossa vida como a base 10 é uma das mais usadas escreve-se apenas Log 100 = 2, omitindo-se a escrita da base e estamos conversados.
Nada de errado com a definição, mas acho que seria válido perguntar: – de que cartola saiu este coelho?
Em nenhum momento é mostrado ao aluno que a motivação para invenção dos logaritmos foi transformar multiplicações em somas e divisões em subtrações e que isto aconteceu no século XVI quando ainda não tinham sido inventadas as calculadoras eletrônicas e muito menos os computadores.
E como seria a definição de logaritmo de um número usando as ideais de Briggs e Napier?
Podemos escrever
Definição aritmética de logarítmo
É importante que a razão da PA seja um para que a base do logaritmo coincida com a razão da PG.
Vale ressaltar que poderíamos utilizar outra razão diferente de um para a PA, entretanto o sistema de logaritmos passaria a ter uma base que não coincidiria mais com a razão da PG e deixaria de ter utilidade prática e sim, apenas teórica.
Ah! Então, acho que não resta dúvida que aqueles dois sujeitos tiveram uma ideia genial.
Mas não ficou por aí, Briggs, como eu já disse, passou grande parte de sua vida elaborando uma tabela que permitia fazer os cálculos usando logaritmos porque era preciso encontrar o logaritmo de outros números.
Estas tabelas eram usadas pelos alunos do científico (hoje ensino médio) até por volta dos 70 ou 80 quando as calculadoras ainda não eram comuns como hoje.
Não irei tratar da construção destas tabelas aqui, pois não têm interesse para este post. Agora que sabemos de onde isto saiu podemos usar uma calculadora para nos ajudar na hora de encontrar o logaritmo de algum número diferente de 10, 100 e assim por diante.
Usando uma calculadora construirei a tabela III com os logaritmos na base 10 dos números inteiros de 2 a 9 porque serão úteis para um projeto que virá a seguir.
Tabela III – Logaritmos decimais de de 2 a 9
Briggs e Napier atiraram no que viram e acertaram no que não viram
Se formos olhar os logaritmos apenas pela perspectiva histórica de Briggs e Napier (o “pai”), chegaremos a conclusão que hoje em dia com calculadoras poderosas e extremamente baratas “made in China” o método que eles inventaram é uma inutilidade.
Entretanto, o logaritmo se tornou uma ferramenta matemática poderosa quando se trata de resolver problemas da Natureza cujo comportamento é exponencial, como, por exemplo, pelo menos os três que foram citados no título do post (existem outros).
Pera aí, mas o que é um “comportamento exponencial”?
Grosso modo podemos dizer que é uma coisa que cresce muito rapidamente, como, por exemplo, a sua divida no cartão de crédito ou no cheque especial, e aí todo brasileiro entende bem o que é “crescer exponencialmente”.
Proponho agora examinarmos as duas progressões (PA e PG) tabela I sob um ponto de vista geométrico.
Escala linear e escala logarítmica
Aqui começaremos a ver os logaritmos de uma forma que interessa particularmente a eletrônica.
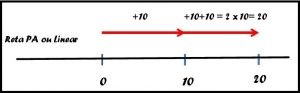
Para isso vou construir duas retas. A primeira que chamarei de reta PA ou escala linear será similar a uma régua começando em zero na qual caminhamos de dez em 10 unidades, neste exemplo.
Escala linear
Observamos que para avançar nesta reta temos que ir somando 10, então para chegar ao 20, somamos 10 e se quiséssemos chegar ao 30 somaríamos mais 10 e assim sucessivamente.
Da mesma forma se estivéssemos no 30 e quiséssemos chegar ao zero teríamos que caminhar para a esquerda subtraindo 10+10+10.
Até aqui creio que não tem nada de mais. Trata-se de uma escala linear similar a uma régua com a qual você está acostumado deste o primário (para os “antigos”) ou fundamental (para os “modernos”).
Escolhi (10) dez em vez de (1) um para facilitar o desenho que vem a seguir.
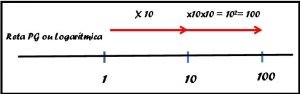
E agora vou construir uma nova reta que chamarei de reta PG ou escala logarítmica e esta começará em um e não em zero como fiz na outra. Você desconfia por quê?
Também vou andar de dez em dez só que agora multiplicando por dez em vez de somar dez. Reparou que estamos “andando” muito mais depressa. Se “andássemos” mais dez unidades chegaríamos ao mil e como mais dez ao dez mil.
Escala logaritimica
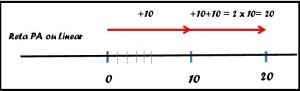
Voltando momentaneamente a reta PA se quiséssemos marcar onde fica o um, o dois o três, etc era só dividir dez por dez e pegar cada pedacinho e colocar um do lado do outro.
Escala linear
E na reta PG ou escala logarítmica onde iremos marca o dois, o três, o quatro e etc?
Este é um raciocínio mais complicado e por isso, temos que pensar um pouco mais.
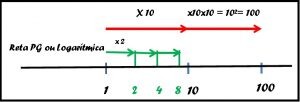
Voltemos a nossa figura da escala logarítmica.
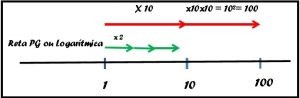
Para ir do um para o dez multiplicamos por dez, então para ir do um para o dois devemos multiplicar por dois (veja o destaque em verde na figura). Até aqui estamos de acordo?
Melhorando a escala logarítmica
A questão é saber onde vai parar o dois.
Vejamos: 101 = 10 e 102 = 100, então parece claro que 10 elevado a algum número entre um e dois, que eu chamarei temporariamente de “?”, teremos 10? = 2.
Em outras palavras, usando a definição de logaritmo, temos que Log 2 = ? (como a base é 10 não precisamos escrever).
Neste caso recorremos a calculadora ou a nossa tabela III e descobrimos que Log 2 = 0,3.
Então a nossa setinha verde anda quase um terço do caminho entre um e dez (um pouquinho menos porque um terço seria 0,3333).
E para chegar ao quatro? Muito fácil, é só andar duas vezes dois que dá quatro e se andar mais duas vezes chegamos ao oito.
Acompanhe na figura a seguir.
Acrescentando outros números na escala logarítimica
Antes de prosseguir para marcar os pontos que estão faltando (3, 5, 6, 7 e 9) quero que você observe como esta escala se comporta de modo bem diferente da escala linear. Note, por exemplo, que o cinco, não vai ficar exatamente na metade do caminho entre o um e dez como acontece na escala linear.
Você seria capaz de marcar os pontos 3, 5, 6, 7 e 9 que estão faltando?
A tabela III pode ajudar nesta missão.
Vou dar uma ajudinha. Na tabela III vemos que que é quase 0,5, ou seja, só um pouquinho antes da metade do caminho entre um e dez.
O que você deve percebido é que a escala logarítmica tem o “poder” de ir “comprimindo” os números à medida que vamos avançando.
Antes de encerrar esta primeira parte, quero convidá-lo a pensar na diferença de comportamento entre um potenciômetro linear e um logarítmico.
No potenciômetro linear quando estamos com o cursor exatamente no centro a resistência entre uma extremidade e o terminal central é exatamente a metade, mas no logarítmico a resistência já teria chegado a quase 70%.
E daí em diante a resistência começa aumentar mais lentamente.
Agora para encerrar por hoje, deixo uma pergunta: – por que é importante usarmos potenciômetros logarítmicos em controle de volume?
No próximo post tratarei do decibel entre outras coisas.
Até sempre.
Algumas referências (as outras estão na minha memória!)
Farias, Sinésio – Curso de Álgebra – Editora Globo -1ª edição – 9ª impressão – 1959 – págs. 856 e seg.
Boyer, C. História da Matemática – Editora Edgard Blucher – 2ª edição – 1996 – pag.213 e segs.
http://www.ppgecnm.ccet.ufrn.br/publicacoes/publicacao_40.pdf
https://www.youtube.com/watch?v=bXzgwh_M0Kw
6 Comentários